今回は, 『グラフ・ネットワークアルゴリズムの基礎 数理とCプログラム』の「第7章 最短パス」のダイクストラのアルゴリズムで紹介されている C のプログラムを Python に移植したという話です。実装の目的はコード化することで理解が曖昧な点を極力減らしていくことです。環境は Python 3.7 です。
グラフ表現のデータ構造
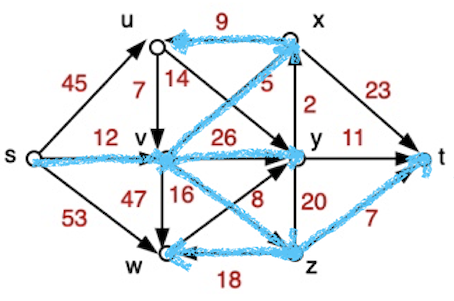
グラフ (graph) はノード (node, vertex) とノードを結ぶエッジ (edge) で構成される数理モデルである。グラフ G はノードの集合 V とエッジの集合 E として G= (V, E) と表記されることが多い。今回は, 本書の第7章で用いられている以下の有向グラフ (directed graph) を扱う。赤字はノードから別のノードへのパス (path) の長さ (又は距離やコスト) を表す。

グラフのデータ構造は, 始点 (tail) と終点 (head) を用いて配列 (Python では list) やポインタで表現できる。行列による表現もできるがグラフが大きくなるに連れて非効率となる。
tail = [1, 1, 1, 2, 2, 3, 3, 3, 3, 4,
5, 5, 6, 6, 6, 7, 7]
head = [2, 3, 4, 3, 6, 4, 5, 6, 7, 6,
2, 8, 5, 7, 8, 4, 8]
length = [45, 12, 53, 7, 14, 47, 5, 26, 16, 8,
9, 23, 2, 20, 11, 18, 7]
tail, head 以外に, すべての辺のリストである接続辺リスト (incidence list) をメモリ上に持っておくと便利である。
tail, head の2つの list から接続辺リストを得る関数は以下のように書ける。
def construct_incidence_list(tail, head):
n = len(set(head + tail))
m = len(head)
edge_first = [0] * n
edge_next = [0] * m
for i in range(m, 0, -1):
v = tail[i-1]
edge_next[i-1] = edge_first[v-1]
edge_first[v-1] = i
return edge_first, edge_next
以下の接続辺リストが得られる。
[1, 4, 6, 10, 11, 13, 16, 0] # edge_first
[2, 3, 0, 5, 0, 7, 8, 9, 0, 0, 12, 0, 14, 15, 0, 17, 0] # edge_nexttail, head に加えて tail から head 方向の接続辺リストを用いた表現は, 有向グラフの標準的データ構造 (standard data structure) と呼ばれる。
ダイクストラのアルゴリズム
最短パス問題のひとつに, 与えられた始点 s からすべてのノードへの最短パスを求める問題がある。長さが負となる閉路が存在しない場合, s から各ノードへの最短パスは s を根 (root) とする根付き木 (rooted tree) で表現でき, これを最短パス木 (shortest path tree) という。
最短パス木を求める有名なアルゴリズムとして, ダイクストラ (E.W. Dijkstra) により提案されたアルゴリズムがある。一言で表すと, s から各ノードに対して最短パスを短い順に求め確定していく方法である。
本書から引用したダイクストラのアルゴリズムは以下である。ここで VP は s から最短パスが確定したノードの集合, V(G) – VP は最短パスが未確定のノードの集合とする。また, s から v までの最短パスの距離と最後のエッジを管理するリストを distance[v], path[v] とする。
- 出発点 s を選び, VP := ∅; distance[s] := 0; path[s] :=0; とする. s 以外の点 v に対しては, distance[v] := ∞; path[v] := -1; とする.
- VP ≠ V(G) である限り 3, 4 を繰り返す
- V(G) – VP の点の内で distance の値の最小な点 w を求める.
- VP := VP ∪ {w} とする. さらに w を始点とする各辺 e = (w, v) ∈ δ+(w ) に対して, distance[v] > distance[w] + length(e) ならば, distance := distance[w] + length(e); path[v] := e とする.
手順 3 は貪欲法 (greedy algorithm) に対応しており, アルゴリズムが進むにつれて未確定のノード v の distance[v] は単調減少し, 確定した後は変化しない。
対象のノード v から distance[v] が最小のノードを見つける際に, ヒープ (優先度付きキューを根付き木で実現) の最小値の要素が常に根となる性質 (i.e. O(1))を活かし計算時間を効率化できる。個人的には, ヒープの解説は「ヒープをわかりやすく解説してみた」が分かり易いと思う。
Python で実装
7.4 節の C で書かれたダイクストラのアルゴリズムをほとんどそのまま Python に移植してみる。移植にあたり, 部分的にゼロベースのインデックス化 (zero-based indexing) に変更している点や変数名, 関数名以外はほぼそのままである。
# -*- coding: utf-8 -*-
UNVISITED = -1
def construct_incidence_list(tail, head):
n = len(set(head + tail))
m = len(head)
edge_first = [0] * n
edge_next = [0] * m
for i in range(m, 0, -1):
v = tail[i-1]
edge_next[i-1] = edge_first[v-1]
edge_first[v-1] = i
return edge_first, edge_next
def main():
tail = [1, 1, 1, 2, 2, 3, 3, 3, 3, 4,
5, 5, 6, 6, 6, 7, 7]
head = [2, 3, 4, 3, 6, 4, 5, 6, 7, 6,
2, 8, 5, 7, 8, 4, 8]
length = [45, 12, 53, 7, 14, 47, 5, 26, 16, 8,
9, 23, 2, 20, 11, 18, 7]
start = 1
edge_first, edge_next = construct_incidence_list(tail, head)
n = len(set(head + tail))
heap = [0] * (n+1)
inv_heap = [0] * (n+1)
distance = [0] * (n+1)
def shift_down(p, q):
while 2*p <= q:
r = 2 * p
if (r+1 <= q) and (distance[heap[r+1]] < distance[heap[r]]):
r = r + 1
if distance[heap[p]] > distance[heap[r]]:
inv_heap[heap[r]] = p
inv_heap[heap[p]] = r
v = heap[p]
heap[p] = heap[r]
heap[r] = v
p = r
else:
p = q
def shift_up(p):
while p > 1:
r = int(p/2)
if distance[heap[p]] < distance[heap[r]]:
inv_heap[heap[r]] = p
inv_heap[heap[p]] = r
v = heap[p]
heap[p] = heap[r]
heap[r] = v
p = r
else:
p = 1
path = [0] + [UNVISITED for v in range(1, n+1)]
distance[start] = 0
path[start] = 0
heap[1] = start
inv_heap[start] = 0
i = 1
while i > 0:
v1 = heap[1]
heap[1] = heap[i]
inv_heap[heap[1]] = 0
i = i - 1
if i > 1:
shift_down(1, i)
edge_to_v2 = edge_first[v1-1]
while edge_to_v2 != 0:
v2 = head[edge_to_v2-1]
dist_tmp = distance[v1] + length[edge_to_v2-1]
if path[v2] == UNVISITED:
distance[v2] = dist_tmp
path[v2] = edge_to_v2
i = i + 1
heap[i] = v2
inv_heap[v2] = i
shift_up(i)
elif distance[v2] > dist_tmp:
distance[v2] = dist_tmp
path[v2] = edge_to_v2
shift_up(inv_heap[v2])
edge_to_v2 = edge_next[edge_to_v2-1]
for v in range(1, n+1):
if v != start:
edge = path[v]
print("ノード {0} までの距離は {1}, パスの最後の辺は長さ {2} でエッジは {3} = ({4}, {5})"
.format(v, distance[v], length[edge-1], edge, tail[edge-1], v))
if __name__ == '__main__':
main()
下移動 (shift_down) でヒープを構成, 上移動 (shift_up) でヒープにノードを挿入し再構成している。実行すると以下の出力が得られる。
$ python dijkstra.py
ノード 2 までの距離は 26, パスの最後の辺は長さ 9 でエッジは 11 = (5, 2)
ノード 3 までの距離は 12, パスの最後の辺は長さ 12 でエッジは 2 = (1, 3)
ノード 4 までの距離は 46, パスの最後の辺は長さ 18 でエッジは 16 = (7, 4)
ノード 5 までの距離は 17, パスの最後の辺は長さ 5 でエッジは 7 = (3, 5)
ノード 6 までの距離は 38, パスの最後の辺は長さ 26 でエッジは 8 = (3, 6)
ノード 7 までの距離は 28, パスの最後の辺は長さ 16 でエッジは 9 = (3, 7)
ノード 8 までの距離は 35, パスの最後の辺は長さ 7 でエッジは 17 = (7, 8)
上記を基に最短パスを辿ってみると, 以下の水色線で示した最短パス木が得られる。
heapq を使う
せっかく Python に移植したので, Python のヒープキューの標準ライブラリ heapq を使う方が全体の見通しは良さそうと考え, heapq でヒープ部分を置き換えた場合が以下。distance とノードを tuple で持つようにしている。置き換え前と同様の結果は得られるが, 本書とは内部的に異なる動作となっている点は注意。
# -*- coding: utf-8 -*-
import heapq
UNVISITED = -1
def construct_incidence_list(tail, head):
n = len(set(head + tail))
m = len(head)
edge_first = [0] * n
edge_next = [0] * m
for i in range(m, 0, -1):
v = tail[i-1]
edge_next[i-1] = edge_first[v-1]
edge_first[v-1] = i
return edge_first, edge_next
def main():
tail = [1, 1, 1, 2, 2, 3, 3, 3, 3, 4,
5, 5, 6, 6, 6, 7, 7]
head = [2, 3, 4, 3, 6, 4, 5, 6, 7, 6,
2, 8, 5, 7, 8, 4, 8]
length = [45, 12, 53, 7, 14, 47, 5, 26, 16, 8,
9, 23, 2, 20, 11, 18, 7]
start = 1
edge_first, edge_next = construct_incidence_list(tail, head)
n = len(set(head + tail))
distance = [0] * (n+1)
path = [0] + [UNVISITED for v in range(1, n+1)]
distance[start] = 0
path[start] = 0
hq = [(0, start)]
heapq.heapify(hq)
while len(hq) > 0:
_, v1 = heapq.heappop(hq)
edge_to_v2 = edge_first[v1-1]
while edge_to_v2 != 0:
v2 = head[edge_to_v2-1]
dist_candidate = distance[v1] + length[edge_to_v2-1]
if path[v2] == UNVISITED or distance[v2] > dist_candidate:
distance[v2] = dist_candidate
path[v2] = edge_to_v2
heapq.heappush(hq, (distance[v2], v2))
edge_to_v2 = edge_next[edge_to_v2-1]
for v in range(1, n+1):
if v != start:
edge = path[v]
print("ノード {0} までの距離は {1}, パスの最後の辺は長さ {2} でエッジは {3} = ({4}, {5})"
.format(v, distance[v], length[edge-1], edge, tail[edge-1], v))
if __name__ == '__main__':
main()
上記を実行すると heapq 置き換え前と同様の結果が得られる。
第7章 演習問題 7.2
演習問題 7.2は, 以下のグラフ (エッジは両方向向き) に対してノード1を始点としてダイクストラのアルゴリズムを実行し最短パス木を求めるという問題である。
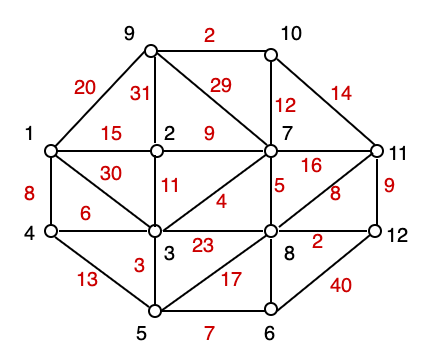
入力データである tail, head, length を以下のように置き換える。
tail = [1, 1, 1, 1, 2, 2, 2, 2, 3, 3,
3, 3, 3, 3, 4, 4, 4, 5, 5, 5,
5, 6, 6, 6, 7, 7, 7, 7, 7, 7,
8, 8, 8, 8, 8, 8, 9, 9, 9, 9,
10, 10, 10, 11, 11, 11, 11, 12, 12, 12]
head = [2, 3, 4, 9, 1, 3, 7, 9, 1, 2,
4, 5, 7, 8, 1, 3, 5, 3, 4, 6,
8, 5, 8, 12, 2, 3, 8, 9, 10, 11,
3, 5, 6, 7, 11, 12, 1, 2, 7, 10,
7, 9, 11, 7, 8, 10, 12, 6, 8, 11]
length = [15, 30, 8, 20, 15, 11, 9, 31, 30, 11,
6, 3, 4, 23, 8, 6, 13, 3, 13, 7,
17, 7, 19, 40, 9, 4, 5, 29, 12, 16,
23, 17, 19, 5, 8, 2, 20, 31, 29, 2,
12, 2, 14, 16, 8, 14, 9, 40, 2, 9]
実行すると以下が出力される。
$ python dijkstra_with_heapq.py
ノード 2 までの距離は 15, パスの最後の辺は長さ 15 でエッジは 1 = (1, 2)
ノード 3 までの距離は 14, パスの最後の辺は長さ 6 でエッジは 16 = (4, 3)
ノード 4 までの距離は 8, パスの最後の辺は長さ 8 でエッジは 3 = (1, 4)
ノード 5 までの距離は 17, パスの最後の辺は長さ 3 でエッジは 12 = (3, 5)
ノード 6 までの距離は 24, パスの最後の辺は長さ 7 でエッジは 20 = (5, 6)
ノード 7 までの距離は 18, パスの最後の辺は長さ 4 でエッジは 13 = (3, 7)
ノード 8 までの距離は 23, パスの最後の辺は長さ 5 でエッジは 27 = (7, 8)
ノード 9 までの距離は 20, パスの最後の辺は長さ 20 でエッジは 4 = (1, 9)
ノード 10 までの距離は 22, パスの最後の辺は長さ 2 でエッジは 40 = (9, 10)
ノード 11 までの距離は 31, パスの最後の辺は長さ 8 でエッジは 35 = (8, 11)
ノード 12 までの距離は 25, パスの最後の辺は長さ 2 でエッジは 36 = (8, 12)
上記を基に最短パス木を水色線で図示すると以下となる。
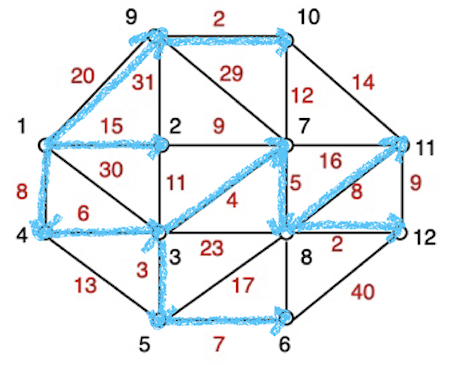
[1] 『グラフ・ネットワークアルゴリズムの基礎』のプログラムファイル
[2] ネットワーク科学―ひと・もの・ことの関係性をデータから解き明かす新しいアプローチ―
