タグ: SVM

【R】SVMの基礎

SVM (Support Vector Machine) はマージン最大化を特徴とした教師あり学習手法です。

線形SVM

SVMでは2つのクラスを分ける分離超平面を求めます。 ω を重みベクトル, γ を切片として各サンプルに対するマージンを正にする ω と γ が存在するとき線形分離可能であるといいます。

    \begin{eqnarray*} f_\omega_\gamma(x) = \omega^Tx+\gamma \end{eqnarray*}

このマージンを最大限に余裕を持って分離する超平面を選択することをマージン最大化といいます。
この分離超平面を求めることは, マージンの逆数の二乗を最小化する最適化問題です。

制約が等式の場合, 最適解を探すのは難しいことからラグランジュの未定乗数法というテクニックを用います。
ラグランジェ関数 L を使うことでラグランジュ関数と制約関数の連立方程式にできるのでこれを解くことで最適解を見つける事ができます。

例えば、以下のようラグランジュ乗数 λを導入して x で偏微分すると連立方程式となりこれを解くと最適解が得られます。

    \begin{eqnarray*} L(x,\lambda) = L(x)+ \lambda_g(x) \end{eqnarray*}

制約が不等式の場合, ラグランジュ関数の最大化は双対問題になります。この場合, 双対問題の最適解を求めることで主問題の最適解を求めることができます。

最適解が見つかれば, ω と γ が定まるので分離超平面が得られます。

上記をハードマージンSVMといいますが, 線形分離不可能な場合には解自体を求めることができない事があります。
そこで, 制約式を緩め誤差項 (スラック変数) を導入することで誤差を許容することをソフトマージンSVMといいます。

この時の誤差の許容度の度合いを C と呼ばれるコストパラメータで調整します。Cを上げるとハードマージンSVMに近づきます。

非線形SVM

ソフトマージンSVM では線形分離不可能な場合でも柔軟に対応できますが, 必ずしも良い分離超平面が求めるとは限りません。
SVMを非線形モデルに拡張する場合, カーネルトリック (Müller et al 2001) と呼ばれる技法を用います。

以下の入力空間に対して,

    \begin{eqnarray*} \{x_i\}_{i=1}^n \end{eqnarray*}

非線形関数 Φ で特徴空間に写像 (map) します。

    \begin{eqnarray*} \{\phi\(x_i\)\}_{i=1}^n \end{eqnarray*}

しかし, 単に高次元空間への写像することは計算量やメモリの点で困難です。
まず, 入力空間でのある2点を x, x’ とした時 カーネル関数は以下で表され, 非線形関数によってD次元空間 (特徴空間 または 再生カーネルヒルベルト空間) に写像された2点 Φ(x), Φ(x’) の内積となります。

    \begin{eqnarray*} K(x, x') = \sum_{k=1}^{D} \phi_{k} (x) \phi_{k} (x') \end{eqnarray*}

この内積計算と同じことが入力空間の(半正定値)カーネル関数によって行えます。例えば, RBFカーネル は以下で示されます。

    \begin{eqnarray*} K(x, x') = \exp(-\frac{||x - x'||^{2}}{\sigma^{2}}) \end{eqnarray*}

高次元の特徴空間で線形モデルで学習を行うことは, 元の空間で非線形のモデルを用いていることと等価となります。
これはカーネルトリックと呼ばれ, 展開がエレガントなこともありカーネル法は広く普及しました。

正則化

訓練データに適合しすぎた結果, 未知のサンプルに対する汎化能力が低いことを過学習 (Overfitting) といいます。過学習を避けるために損失関数に正則化項 (罰則項) を追加することを正則化 (Regularization) といいます。損失関数をどのように設計するかで最終的に得られるアルゴリズムが変わります。ramp 関数と呼ばれる上界を持つ損失関数を用いる事でロバスト性が向上します。

    \[ min\{1,max & (0,1-m) \}= \begin{cases} 1 & (m < 0) \\ 1-m & (0 \leq m \leq 1) \\ 0 & (m > 1) \end{cases} \]

m < 0 の場合を1で打ち切っているのが hinge 関数と異なります。ramp とは高速道路と一般道などの傾斜の段差を繋ぐ傾斜道のことで, ランプ損失の表す 0 と 1 と繋ぐ直線がこれに似ていることから命名されたようです。

RでSVM

Rでは libsvm の wrapper である {kernlab} や {e1071}, {KlaR} でSVMを使えます。 {kernlab} を使って Iris libsvm の versicolor と virginica の2クラス分類を行ってみます。

kernlab::ksvm の type には分類問題の場合は SVC (Support Vector Classification) , 回帰問題の場合は SVR (Support Vector Regression) を指定します。

library(kernlab)

set.seed(1500)

d <- data.frame(iris[51:150,3:4], y = as.character.factor(iris[51:150,5])) # versicolor and virginica
d$y <- setattr(d$y,"levels", c("versicolor", "virginica"))

iris.ksvm <- ksvm(
  y ~ ., # y is Species
  data = d,
  kernel = "rbfdot",
  kpar = list(sigma=0.2), # kernel param sigma
  C = 5, # margin param C
  cross = 3
)

print(iris.ksvm)

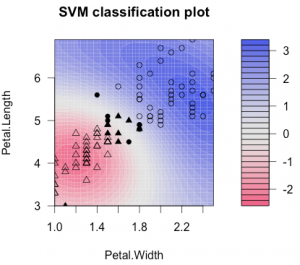
plot(iris.ksvm, data = d[,1:2])

table(d$y, predict(iris.ksvm, d[,1:2]))
#             versicolor virginica
# versicolor         47         3
# virginica           3        47

kernlab_plot

交差検証

交差検証 (Cross-validation; CV) はモデルの汎化能力を検証するためにサンプル集合から汎化誤差を推定する方法です。交差検証によりモデルを選択することで過学習を抑制します。サンプル集合を k 個に分割したときを k 分割交差検証 (k-fold cross-validation) といいます。
k 分割交差検証の分割数 k は kernlab::ksvm の引数 cross に指定します。

分割はサンプル集合を訓練, 検証, テストの3つの集合に分割する方法が適切です。この時, 系列データでない場合は各集合のサンプルの分布が均等になるようにランダムに選択します。k 分割交差検証は訓練集合と検証集合に対して行い, 最終的に得られたモデルをテスト集合に対して1回だけ実行することで, 未知のサンプルに対して期待される品質を適切に推定することができます。

パラメータチューニング

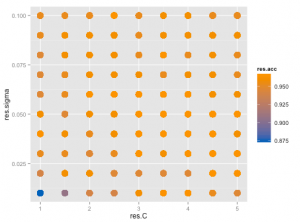
SVMの コストパラメータ C とRBFカーネルのパラメータ sigma のより良い値をグリッドサーチ (Grid Search) で探します。

{caret} は 100以上の機械学習手法や予測モデルに対して評価が行えるRのパッケージです。
caret::train の method でモデルを指定します。trControl で training データ, tuneGrid で Grid Search のカスタマイズも行えます。

library(caret)
library(kernlab)
library(ggplot2)
library(e1071)

grid <- expand.grid(
  C = ((2:10)*0.5),
  sigma = ((1:10)*0.01)
)

ctrl <- trainControl(
  method = "cv",
  savePred = T,
  classProb = T,
  number = 3
)

svmFit <- train(
  Species ~ .,
  data = iris,
  method = "svmRadial", # gaussian kernel
  trace = T,
  trControl = ctrl,
  tuneGrid = grid
)

p <- ggplot(svmFit$results, aes(x = C, y = sigma))
p + geom_point(aes(colour = Accuracy), size = 10) + scale_colour_gradient(low = "#0068b7", high = "#f39800")

grid_search

OCSVM

One Class SVM (Schölkopf et al 2001) は外れ値検出 (Outlier Detection) などで用いられる手法で, カーネルを用いて特徴空間への写像を行うと入力空間での外れ値が特徴空間では原点近くに写像されるという性質を利用し原点とサンプル群を分ける超平面を求めます。
超平面の位置は予め決められた割合 v のサンプル群が原点側に残るように設定されます。通常, 学習時には正常データのみを使用します。

RでOCSVM

OCSVM は ksvm の type に “one-svc” を指定します。 RBFカーネルでは外れ値は特徴空間上の原点側に写像されます。 nu には特徴空間上での原点からのサンプル群の割合を指定します。

set.seed(1500)

df <- data.frame(miles = airmiles[1:24], class = 1)

svm <- ksvm(
  x = class ~ .,
  data = df,
  type = "one-svc",
  kernel = "rbfdot",
  kpar = list(sigma = 0.1),
  nu = 0.1 # 10% from the origin
)

preds <- predict(svm)
pred <- ifelse(preds == TRUE, 1, 0)
res <- data.frame(df, pred)
res$idx <- seq.int(nrow(res))

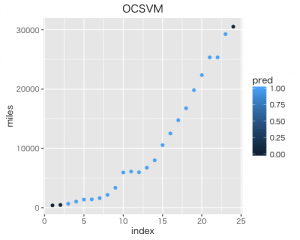
g <- ggplot(res, aes(x = idx, y = miles, colour = pred)) + geom_point() +
  labs(title = "OCSVM", x = "index", y = "miles")
plot(g)

結果は以下です。

参考書籍は『パターン認識と学習の統計学－新しい概念と手法』です。


[1] SVMの双対問題について
[2] SVM回帰
[3] 過学習を防ぐ正則化
[4] caret package
[5] SMO徹底入門 – SVMをちゃんと実装する