今回は生存時間解析の基本的な道具であるカプラン・マイヤー推定量, ログ・ランク検定, Cox 比例ハザードモデルについて Python の lifelines で試してみました。環境は以下です。
- Python 3.7
- numpy 1.17.2
- pandas 0.25.3
- lifelines 0.24.4
- matplotlib 3.0.3
参考書籍は 『生存時間解析入門 原書第2版』です。本書は主に, 生存時間データの回帰モデリングに焦点が当てられています。この記事では理論的な側面には触れないので興味のある方は本書や参考文献をご覧ください。また, lifelines の使い方は Quickstart と Introduction to survival analysis が参考になりました。
生存時間解析
生存時間解析 (survival analysis) は生存時間 (time-to-event) を対象とした解析手法で, 医学・疫学・健康科学・工業製品の故障予測・会員サービスの解約予測など応用分野が広い。打ち切り (censoring) を含む不完全な観測値を扱うことが生存時間解析の大きな特徴である。
データセット
今回は, 趣味で運営している株主優待を検索する iOS アプリの利用データを用いて生存時間解析を試してみる。 この iOS アプリではアプリ利用状況を把握するために, 利用ログを Web サーバに送信している。Web サーバのアクセスログを加工し, 以下の pandas.DataFrame を得る。
In [13]: df_duration
Out[13]:
date_start date_end add_fav_sum add_fav_within_day durations event
1 2019-07-02 08:52:40 2019-07-02 08:53:12 0 False 0.000370 True
2 2019-05-15 08:04:45 2020-02-05 19:34:21 0 False 266.478889 True
3 2019-12-11 19:27:32 2019-12-24 08:33:15 0 False 12.545637 True
4 2019-12-22 17:33:58 2019-12-31 23:36:54 0 False 9.252037 True
6 2019-10-03 08:52:53 2020-03-02 19:50:38 1 False 151.456771 True
... ... ... ... ... ... ...
1265 2020-02-24 22:47:17 2020-03-03 21:21:19 0 False 7.940301 True
1266 2020-02-22 04:27:21 2020-04-11 07:51:14 3 False 49.141586 False
1267 2020-04-22 07:18:30 2020-04-22 07:21:12 0 False 0.001875 False
1268 2019-11-13 14:19:28 2020-02-24 20:29:02 0 False 103.256644 True
1269 2019-11-21 17:26:43 2019-11-21 17:49:47 0 False 0.016019 True
[1121 rows x 6 columns]各列の意味は以下の通り。
- date_start: 最初のアプリ利用日時
- date_end: 観測期間中の最後のアプリ利用日時
- add_fav_sum: お気に入り追加の合計数
- add_fav_within_day: 利用開始後 1 日以内にお気に入り追加をしたか否か (名義尺度)
- durations: 最初の利用から観測期間中の最後の利用までの日数
- event: 利用停止の有無
アプリの最終利用から 30 日間利用が無かった場合を利用停止 (i.e. event) とし, 観測期間中 (過去約1年) に利用停止が発生しなかった場合を右側打ち切りとした。また, 1回のみ利用は分析対象から除いている。
アプリには銘柄のお気に入り追加機能があり, アプリ利用開始後 1 日以内にお気に入りを追加したか否か (add_fav_within_day 列) を共変量と置いた。これは, お気に入り追加を行った場合, その後も株価チェックなどの目的で利用を継続するのではという事前の仮説を調べたかったからである。
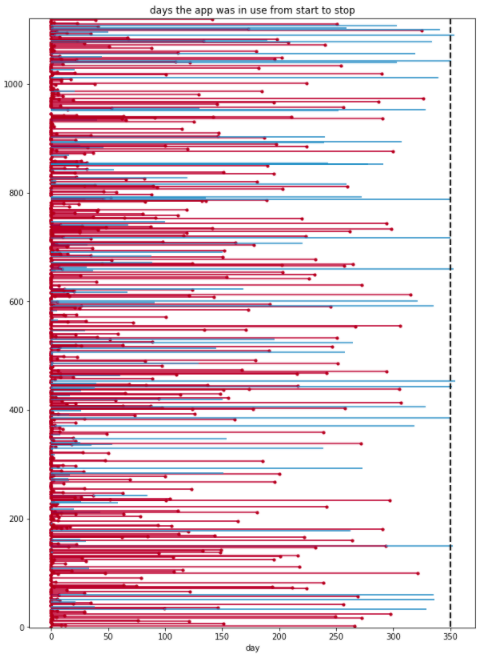
以降の分析で, 期間 (durations 列) とイベント発生有無 (event 列) は最低限必要となる列である。最初に生存時間と打ち切り状況を可視化する。
from lifelines.plotting import plot_lifetimes
fig, ax = plt.subplots(figsize=(10, 14))
ax = plot_lifetimes(df_duration["durations"], event_observed=df_duration["event"])
ax.set_xlabel("day")
ax.set_title("days the app was in use from start to stop")
ax.vlines(350, 0, 1130, lw=2, linestyles='--')
plt.show()
カプラン・マイヤー推定量
生存関数 S(t) は, ある時間 t よりも大きい生存時間が与えられる確率である。 カプラン・マイヤー推定量 (Kaplan Meier estimator) を用いて生存関数を推定する。カプラン・マイヤー推定量は打ち切りでない観測値と打ち切りの観測値の両方の情報を含んでいる。
lifelines の KaplanMeierFitter クラスでカプラン・マイヤー推定量を得て, 信頼区間付きでプロットする。
from lifelines import KaplanMeierFitter
kmf = KaplanMeierFitter()
kmf.fit(df_duration['durations'], df_duration['event'], label='Kaplan Meier Estimate')
kmf.plot(ci_show=True)
KaplanMeierFitter のインスタンスから生存時間分布の分位点を取り出すこともできる。
次に, 共変量 (開始後 1 日以内のお気に入り追加の有無) で二群に分け, 生存関数のカプラン・マイヤー推定量をプロットする。
kmf = KaplanMeierFitter()
T = df_duration["durations"]
E = df_duration['event']
groups = df_duration['add_fav_within_day']
ix1 = (groups == False)
ix2 = (groups == True)
kmf.fit(T[ix1], E[ix1], label='add_fav_within_day is False')
ax = kmf.plot()
kmf.fit(T[ix2], E[ix2], label='add_fav_within_day is True')
kmf.plot(ax=ax)
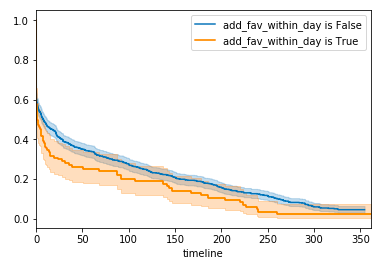共変量 (開始後 1 日以内のお気に入り追加) 有りのグループは全体の 11.5 %と少ないため信頼区間の幅は広くなっている。 事前の予想に反し, 1 日以内のお気に入り追加を行った場合の方が2週間前後までに利用を停止する確率が高いことが窺える。
ログ・ランク検定
1 日以内のお気に入り追加を共変量として, 生存関数の差の有無についてログ・ランク (log-rank) 検定を行う。
In [16]: from lifelines.statistics import logrank_test
...:
...: results = logrank_test(T[ix1], T[ix2], E[ix1], E[ix2], alpha=.95)
...: results.print_summary()
t_0 = -1
null_distribution = chi squared
degrees_of_freedom = 1
alpha = 0.95
test_name = logrank_test
---
test_statistic p -log2(p)
2.60 0.11 3.23
検定統計量 (カイ二乗統計量) は 2.60, p 値は 0.11 で, 開始後 1 日以内のお気に入り追加は生存関数の差に影響しているとは言いにくい。
Cox 比例ハザード・モデル
ハザード関数 h(t,x,β) は時間 t まで生存という条件下で次の時間にイベントが発生する確率である。共変量 x を考慮しないときのハザード関数を基準ハザード関数 h_0(t) という。また, 累積ハザード関数 H(t,x,β) はハザード関数の時間 t までの積分である。
共変量で分けた2つのハザード関数の比をハザード比 HR という。パラメータ推定は回帰分析の枠組みで回帰係数 β を最尤法で推定することが考えられるが, 比例ハザードモデルの (対数) 尤度関数の最大化はできないので, 一般的には部分尤度関数の最大化によりパラメータ推定を行う。
最初に, durations, event, 共変量のみの pandas.DataFrame を作る。今回は共変量は単変量であるが, 多くの回帰分析同様に多変量や交互作用を扱うケースの方が多いと思う。
In [17]: data = df_duration[['durations', 'event', 'add_fav_within_day']]
...: data.loc[:,'add_fav_within_day'] = data['add_fav_within_day'].astype(int)
...: data
Out[17]:
durations event add_fav_within_day
1 0.000370 True 0
2 266.478889 True 0
3 12.545637 True 0
4 9.252037 True 0
6 151.456771 True 0
... ... ... ...
1265 7.940301 True 0
1266 49.141586 False 0
1267 0.001875 False 0
1268 103.256644 True 0
1269 0.016019 True 0
[1121 rows x 3 columns]lifelines の CoxPHFitter クラスを用いて Cox 比例ハザードモデル (Cox proportional hazard model) のモデリングを行える。
In [18]: from lifelines import CoxPHFitter
...:
...: cph = CoxPHFitter()
...: cph.fit(data, duration_col='durations', event_col='event')
...: cph.print_summary()
duration col = 'durations'
event col = 'event'
baseline estimation = breslow
number of observations = 1121
number of events observed = 949
partial log-likelihood = -5832.97
time fit was run = 2020-05-10 01:45:10 UTC
---
coef exp(coef) se(coef) coef lower 95% coef upper 95% exp(coef) lower 95% exp(coef) upper 95%
add_fav_within_day 0.16 1.18 0.10 -0.04 0.36 0.96 1.44
z p -log2(p)
add_fav_within_day 1.61 0.11 3.22
---
Concordance = 0.50
Log-likelihood ratio test = 2.49 on 1 df, -log2(p)=3.12比例ハザード性の検証
Cox 比例ハザードモデルでは, ハザード比を相対リスク (共変量の影響の効果) として解釈できる利点がある。 (e.g. 男性は女性の n 倍死亡率が高い)
一方で, 比例ハザードモデルにより推定されたハザード比は時間に依存せず常に一定 (比例ハザード性の仮定) であるため, 共変量の効果が時間と共に変化する場合は比例ハザードモデルの適用は不適切である可能性がある。
今回の例でも, 開始後 1 日以内のお気に入り追加という共変量は開始時点 t_0 における差ではなく, また時間が経つに連れてお気に入り銘柄の株価に対する興味が徐々に薄れていくことも考えられるかもしれない。このような場合, 比例ハザード性を検証する必要がある。検証方法には以下の方法などがある。
- 共変量ごとの仮説検定 (個々の共変量に対しては Wald 検定, 全体の比例ハザード性に対しては部分尤度比検定)
- スケール化 Schoenfeld 残差とそれを平滑化した曲線のプロット
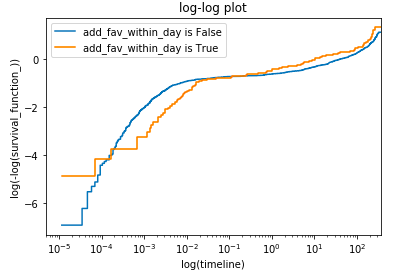
- 生存関数の二重対数プロット
二重対数プロットでは共変量の有無で分けた二群間において生存関数を二重対数でプロットし曲線の距離が時間によらず一定であるかを検証する。2つの曲線が交わらずに平行移動 (等距離を維持) している状態は比例ハザード性が成り立っていることを支持する。
今回の例では以下となった。曲線が交差しており妥当とは言えないことがわかる。
kmf_0 = KaplanMeierFitter()
kmf_0.fit(T[ix1], E[ix1])
kmf_1 = KaplanMeierFitter()
kmf_1.fit(T[ix2], E[ix2])
fig, ax = plt.subplots()
kmf_0.plot_loglogs(ax=ax)
kmf_1.plot_loglogs(ax=ax)
ax.legend(['add_fav_within_day is False', 'add_fav_within_day is True'])
plt.title("log-log plot")
plt.show()
比例ハザード性を満たさない場合の対処法として, 参考書籍の 「第7章 比例ハザードモデルの拡張」 では, 比例ハザードモデルを一般化し, 時間依存性共変量 (time varying covariates) をモデルに含める方法について解説されている。
時間依存性共変量には内的と外的なものがあり, 内的時間依存性共変量は測定された共変量が経時的に変化するもの, 外的間依存性共変量は年齢などの全ての被験者に対して適用されるものを指す。
データが右側打ち切りの場合, 単純に共変量 x に時点 t の情報を取り入れ x(t) としたり, 時間に依存した回帰係数 β(t) とする方法がある。そのうち試してみようと思う。
また, 比例ハザードモデルのモデル診断のひとつに Schoenfeld 残差がある。Schoenfeld 残差は対数尤度の偏導関数に対する各データの寄与に基づく残差である。
[1] 生存時間解析入門
[2] 比例ハザードモデルはとってもtricky！
[3] Survival Analysis: Intuition & Implementation in Python
[4] 生存時間解析におけるセミパラメトリック推測とその周辺
[5] scikit-survival