2015-09-04 に行われた, 「統計的言語研究の現在」で, 久保先生のご講演「カウントデータの統計モデリング入門」を拝聴したので, Rでトレースしてみました。間違いを見つけたらご指摘頂ければと思います。
はじめに
カウントデータ (count data) は非負の離散値のデータ。
2つのコーパス X0と X1において, 単語の品詞カテゴリ {A, B, C…I} の出現頻度が記録された架空のデータにおいて, コーパス間の各品詞カテゴリの出現頻度に差があるのかを分析する。たぶん単語の出現頻度と読み替えても良いと思うけど, ほとんどスパースになる気もするので品詞としていると思う。
Category
X A B C D E F G H I
0 62 21 14 11 10 10 2 0 2
1 48 34 22 17 16 7 2 1 1
2×2分割表の分析
本題の2×9分割表を考える前により小さな問題として 2×2分割表から始める。検定が今回のテーマではないので, カイ二乗検定の話題は省略。
require(lattice)
# 2 x 2
d2 <- read.csv('data/d2x2.csv')
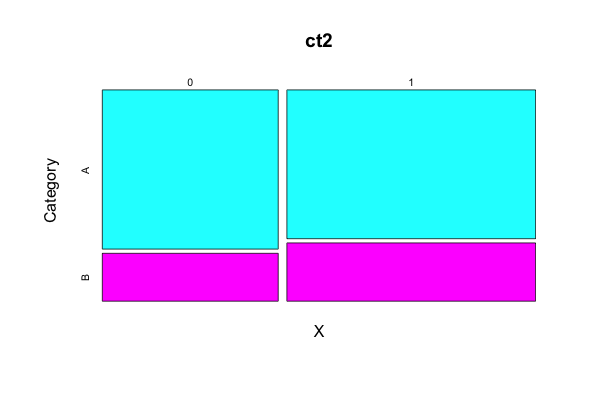
ct2 <- xtabs(y ~ X + Category, data=d2)
plot(ct2 , col=c('cyan', 'magenta'))
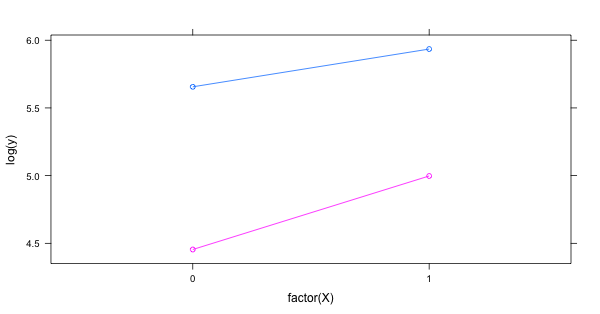
xyplot(log(y) ~ factor(X), data = d2, groups = Category, type = 'b')
model.glm <- glm(ct2 ~ c(0,1), family = binomial)
summary(model.glm)
xtabsで分割表をつくり, plotで表示。
Category
X A B
0 286 86
1 378 148
lattice::xyplot でコーパス間の各品詞カテゴリの出現頻度を確認する。
一般化線形モデル (GLM) のロジスティック回帰, ポアソン回帰でパラメータを推定する。
一般化線形モデルでは, 目的変数を変換する, リンク関数 (link function) を使う。リンク関数は単調かつ微分可能な関数である。
リンク関数を g(μ), デザイン行列を X, パラメータベクトルを β とすると下記で表すことができる。
ロジスティック回帰では, リンク関数 g にロジット関数を用いる。
以下のような 2×2分割表 では, オッズ比 (Odds Ratio, OR) は (ad) / (bc) で計算できる。
> matrix(c("a", "b", "c", "d"), ncol = 2)
[,1] [,2]
[1,] "a" "c"
[2,] "b" "d"
対数オッズ比 (log OR) を求めると下記となり, これがロジスティック回帰の偏回帰係数 β となる。
# coef
> log((286*148) / (86*378))
[1] -0.2639626
# std error
> sqrt(1/286 + 1/86 + 1/378 + 1/148)
[1] 0.1566099
この偏回帰係数は, アナロジー的には線形回帰の傾きに相当する。対数オッズ比の exp を取ると オッズ比となるので確率の比として解釈がしやすくなる。また, 対数オッズ比と標準誤差 (SE)から信頼区間が求まり, exp を取ったオッズ比の信頼区間が 1 を含むかも確認する。
glm() では下記のように書ける。
> model.glm <- glm(ct2 ~ c(0,1), family = binomial(link = logit))
> summary(model.glm)
Call:
glm(formula = ct2 ~ c(0, 1), family = binomial(link = logit))
Deviance Residuals:
[1] 0 0
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.2016 0.1230 9.771 <2e-16 ***
c(0, 1) -0.2640 0.1566 -1.685 0.0919 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2.8725e+00 on 1 degrees of freedom
Residual deviance: 5.0626e-14 on 0 degrees of freedom
AIC: 16.537
Number of Fisher Scoring iterations: 3
ポアソン回帰では一般的に, リンク関数 g(λ) に対数 (log) を用いる。品詞カテゴリAのみでモデリング。(分割モデルA)
Call:
glm(formula = y ~ X, family = poisson, data = d2[d2$Category == "A", ])
Deviance Residuals:
[1] 0 0
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.65599 0.05913 95.652 < 2e-16 ***
X 0.27890 0.07837 3.559 0.000373 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1.2788e+01 on 1 degrees of freedom
Residual deviance: 5.8620e-14 on 0 degrees of freedom
AIC: 19.268
Number of Fisher Scoring iterations: 2
ポアソン回帰, 品詞カテゴリBのみでモデリング。(分割モデルB)
Call:
glm(formula = y ~ X, family = poisson, data = d2[d2$Category == "B", ])
Deviance Residuals:
[1] 0 0
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.4543 0.1078 41.308 < 2e-16 ***
X 0.5429 0.1356 4.004 6.24e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1.6625e+01 on 1 degrees of freedom
Residual deviance: -2.6645e-15 on 0 degrees of freedom
AIC: 17.13
Number of Fisher Scoring iterations: 2
ポアソン回帰, 交互作用あり版でモデリング。(一括モデル)
model.glm <- glm(y ~ X * Category, data=d2, family=poisson)
summary(model.glm)
一括モデルの結果が下記である。
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.65599 0.05913 95.652 < 2e-16 ***
X 0.27890 0.07837 3.559 0.000373 ***
CategoryB -1.20164 0.12298 -9.771 < 2e-16 ***
X:CategoryB 0.26396 0.15661 1.685 0.091896 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 2.4401e+02 on 3 degrees of freedom
Residual deviance: 1.3323e-15 on 0 degrees of freedom
AIC: 36.398
分割モデルAの推定値 (Intercept) 5.65599 と X 0.27890 が一括モデルと一致しており, 分割モデルBの推定値 (Intercept) 4.4543 と X 0.5429 はそれぞれ一括モデルの (Intercept) – CategoryB と X + X:CategoryB に一致している。
2×3分割表の分析
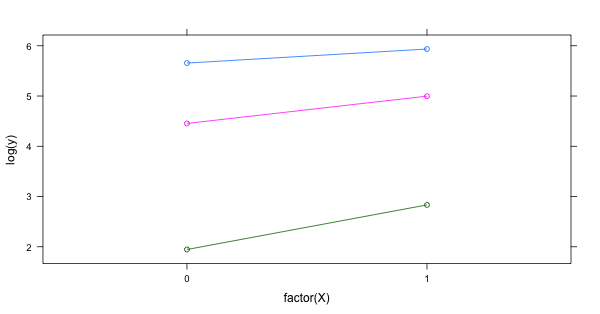
続いて, カテゴリを1つ追加した2×3 分割表について。追加したカテゴリCは各コーパスで出現頻度がA, Bと比べ出現回数が極端に低くなっている。
Category
X A B C
0 286 86 7
1 378 148 17
2×2同様にxyplotで表示。
多項分布 (三項分布) になるが, まずはポアソン回帰。
Call:
glm(formula = y ~ X * Category, family = poisson, data = d3)
Deviance Residuals:
[1] 0 0 0 0 0 0
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.65599 0.05913 95.652 < 2e-16 ***
X 0.27890 0.07837 3.559 0.000373 ***
CategoryB -1.20164 0.12298 -9.771 < 2e-16 ***
CategoryC -3.71008 0.38256 -9.698 < 2e-16 ***
X:CategoryB 0.26396 0.15661 1.685 0.091896 .
X:CategoryC 0.60840 0.45588 1.335 0.182015
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 8.0676e+02 on 5 degrees of freedom
Residual deviance: 5.9952e-15 on 0 degrees of freedom
AIC: 48.887
glmではロジスティック回帰で多項分布を指定できないので nnmet::multnom を使う。
multinom(ct3 ~ c(0, 1))
ポアソン回帰とほぼ同じ結果が得られた。
#weights: 9 (4 variable)
initial value 1012.920530
iter 10 value 624.205679
final value 624.205639
converged
Call:
multinom(formula = ct3 ~ c(0, 1))
Coefficients:
(Intercept) c(0, 1)
B -1.201520 0.2638671
C -3.709631 0.6076266
Residual Deviance: 1248.411
AIC: 1256.411
2×9分割表の分析
冒頭に書いた, 2つのコーパス X0と X1において, 単語の品詞カテゴリ{A, B, C…I} の出現頻度を記録した架空データについて考える。
Category
X A B C D E F G H I
0 62 21 14 11 10 10 2 0 2
1 48 34 22 17 16 7 2 1 1
コーパスX0には, カテゴリHが一度も出現していない。
2×3分割表と同様に, まずはポアソン回帰で分析してみる。
require(lattice)
require(glmmML)
d9 <- read.csv('data/d2x9.csv')
ct9 <- xtabs(y ~ X + Category, data=d9)
plot(ct9)
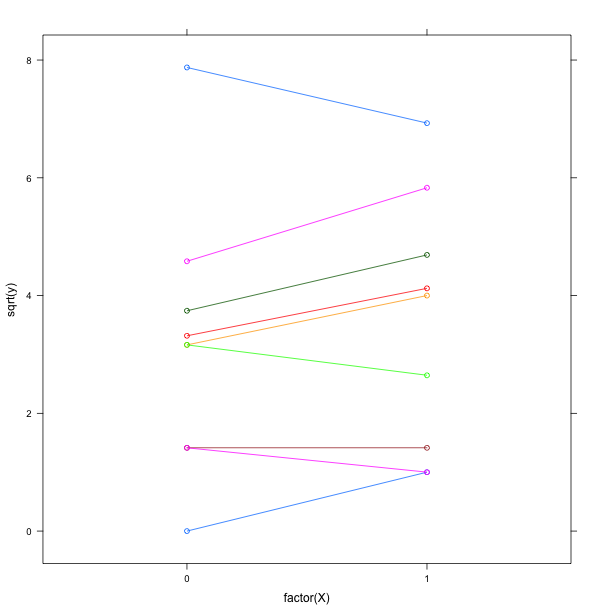
xyplot(sqrt(y) ~ factor(X), data = d9, groups = Category, type = 'b')
model.glm <- glm(y ~ X * Category, data = d9, family = poisson)
summary(model.glm)
分割表が大きくなった時, カテゴリ (個体)によるバラツキが大きいような過分散が起きている場合では, パラメータの推定値の信頼性がバラバラになってしまう。特に0を含むスパースな部分を上手く推定することが難しい。例えば, ポアソン回帰だと CategoryHの推定値が -26.4 であるが, expの中をいくら小さくしても実際の値である 0とはならない。
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.1271 0.1270 32.497 < 2e-16 ***
X -0.2559 0.1923 -1.331 0.1831
CategoryB -1.0826 0.2525 -4.288 1.80e-05 ***
CategoryC -1.4881 0.2959 -5.029 4.93e-07 ***
CategoryD -1.7292 0.3272 -5.285 1.25e-07 ***
CategoryE -1.8245 0.3408 -5.354 8.60e-08 ***
CategoryF -1.8245 0.3408 -5.354 8.60e-08 ***
CategoryG -3.4340 0.7184 -4.780 1.75e-06 ***
CategoryH -26.4297 42247.1657 -0.001 0.9995
CategoryI -3.4340 0.7184 -4.780 1.75e-06 ***
X:CategoryB 0.7378 0.3376 2.185 0.0289 *
X:CategoryC 0.7079 0.3922 1.805 0.0711 .
X:CategoryD 0.6913 0.4321 1.600 0.1096
X:CategoryE 0.7259 0.4466 1.625 0.1041
X:CategoryF -0.1007 0.5290 -0.190 0.8490
X:CategoryG 0.2559 1.0183 0.251 0.8016
X:CategoryH 22.5585 42247.1657 0.001 0.9996
X:CategoryI -0.4372 1.2397 -0.353 0.7243
glmの限界を感じはじめたので, 個体差も考慮するようなモデルを考える。
一般化線形混合モデル(GLMM)で, 線形予測子を全体を表現するパラメータ(global param)と個体差を表現するパラメータ (local param)に分離する。{glmmML}を使う。
model.glmm <- glmmML(y ~ X, data=d9, cluster = Category, family = poisson)
summary(model.glmm)
summary()で全体的なパラメータの推定値が出力される。また, posterior.modesは Estimated posterior modes of the random effects. なので直訳すると, 推定されたランダム効果の事後分布の最頻値 となると思うが, 個体差のパラメータが出力される。
Call: glmmML(formula = y ~ X, family = poisson, data = d9, cluster = Category)
coef se(coef) z Pr(>|z|)
(Intercept) 2.0117 0.4654 4.3227 1.54e-05
X 0.1144 0.1197 0.9557 3.39e-01
Scale parameter in mixing distribution: 1.33 gaussian
Std. Error: 0.314
LR p-value for H_0: sigma = 0: 5.561e-54
Residual deviance: 50.71 on 15 degrees of freedom AIC: 56.71
model.glmm$posterior.modes
[1] 1.9268622 1.2309349 0.8070984 0.5572246 0.4838544 0.0673045 -1.2185223 -2.0058464 -1.4269678
glmmML()によって glm() におけるゼロデータ問題は解決できたが, より複雑な階層ベイズモデルに対して扱うのは難しくなってくる。
そこで, MCMC法によるベイジアンモデリングが登場する。MCMCでパラメータの事後分布のサンプリングを行う。
今回, MCMCサンプラーはJAGSではなく, Stanで試してみる。
stan_code <- '
data {
int<lower=1> n;
int x[n];
int<lower=0> y[n];
}
parameters {
real a0;
real b1;
vector[n] r;
real s_r;
}
model {
for(i in 1:n) {
y[i] ~ poisson_log(a0 + b1 * x[i] + r[i]);
r[i] ~ normal(0, s_r);
}
}
'
d <- list(
n=9,
y=d9$y[0:9], # [1] 62 21 14 11 10 10 2 0 2
x=d9$y[0:9] - d9$y[10:18] # [1] 14 -13 -8 -6 -6 3 0 -1 1
)
d.fit <- stan(model_code=stan_code, data=d, iter=1000, chains=4)
print(d.fit, digit=2)
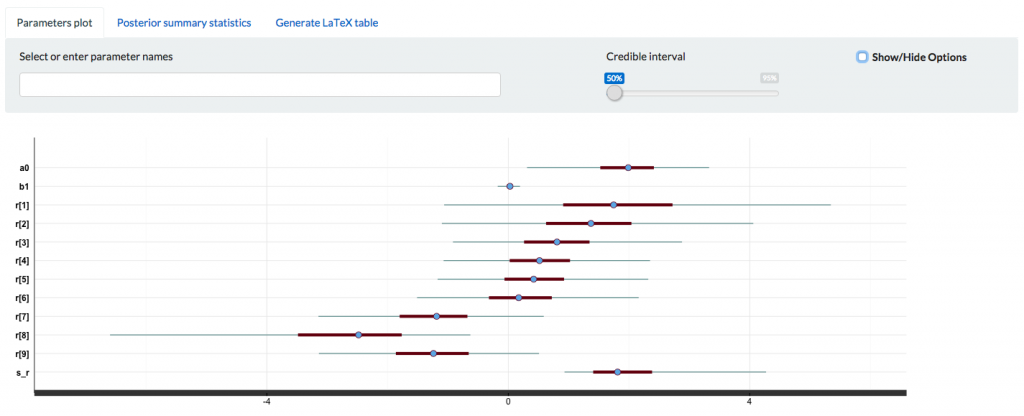
</lower=0></lower=1>CategoryD, Eは信用区間の幅が狭く確信度が強い一方で, 特にCategoryHは幅が広くなっており確信度が弱くなっている。
Inference for Stan model: stan_code.
4 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=2000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
a0 1.95 0.04 0.74 0.31 1.52 1.99 2.41 3.33 405 1.01
b1 0.02 0.00 0.09 -0.18 -0.03 0.03 0.08 0.19 576 1.00
r[1] 1.83 0.07 1.65 -1.06 0.91 1.75 2.72 5.35 539 1.01
r[2] 1.37 0.06 1.23 -1.10 0.63 1.37 2.04 4.06 446 1.00
r[3] 0.83 0.04 0.92 -0.92 0.26 0.81 1.35 2.88 454 1.00
r[4] 0.54 0.04 0.84 -1.07 0.02 0.52 1.02 2.35 414 1.00
r[5] 0.44 0.04 0.83 -1.17 -0.06 0.42 0.92 2.32 470 1.00
r[6] 0.22 0.04 0.90 -1.51 -0.32 0.17 0.72 2.16 485 1.01
r[7] -1.23 0.04 0.93 -3.15 -1.80 -1.19 -0.68 0.59 543 1.01
r[8] -2.78 0.07 1.49 -6.60 -3.48 -2.48 -1.77 -0.63 490 1.00
r[9] -1.27 0.04 0.96 -3.14 -1.86 -1.24 -0.66 0.51 504 1.00
s_r 2.00 0.05 0.86 0.93 1.41 1.81 2.38 4.27 287 1.01
lp__ 285.63 0.17 2.96 279.18 283.87 285.98 287.78 290.40 312 1.02
Samples were drawn using NUTS(diag_e) at Mon Sep 7 22:20:56 2015.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
stanfit objectを shinystan::launch_shinystan() で localhost にサービスが起動するのでブラウザからアクセスする。[1]
おわりに
参考書籍は『データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)』です。
[1] shinystan
[2] ポアソン分布に従うのは生起頻度が非常に低い事象の観測データで, 仮定として希少性, 定常性(事象の起きる確率は時間帯に依らない), 独立性 (事象の起きる確率はそれ以前の事象と無関係) がある。パラメータ λ は単位時間当たりの平均生起回数。