ADVI in Stan は既に多くの方が試されているのですが, まずは触って理解したいのもあり試してみました。
ちなみに今まで Stan Code をインラインで書いていましたが, ATOM の language-stan を使ったら Stan の syntax highlight がいい感じだったので別ファイルから読み込むようにしました。
ADVIとは
2015年に発表 [1] された ADVI (Automatic Differentiation Variational Inference, 自動変分ベイズ) は 変分下限や近似分布を与えなくても自動的に事後分布の最もよい近似分布を KLダイバージェンス で探索して, その近似事後分布からのサンプルを得ることができる。サンプルが得られれば, MCMC同様に性質を調べることで知りたいパラメータを推定できる。既に Stan に実装があり, NUTSと比較しても, かなり高速だが初期値に敏感など まだヒューリスティックなハックが必要らしい。
と書いたけど, ちゃんと理解しているわけではないので, 詳しい話は [2, 3] などを参照の事。
ADVI in Stan
Eight Schools は米国のSAT (大学進学適性試験)スコアのコーチング効果の分析データで, Bayesian Data Analysis の例でも取り上げられている。
school y se
A 28 15
B 8 10
C -3 16
D 7 11
E -1 9
F 1 11
G 18 10
H 12 18
NUTS と ADVI をStanで動かす。Stanのコードは共通して下記。(公式チュートリアルと同様)
data {
int J; // サンプルサイズ
real y[J]; // コーチング効果
real sigma[J]; // 標準偏差
}
parameters {
real mu; // 定数
real tau; // eta[j] の係数
real eta[J]; // 個体差
}
transformed parameters {
real theta[J];
for (j in 1:J)
theta[j] <- mu + tau * eta[j]; // 個体ごとの平均
}
model {
eta ~ normal(0, 1); // eta は標準正規分布に従う
y ~ normal(theta, sigma); // y は N(theta, sigma)に従う
}
NUTS
まずは NUTS で動かしてみる。
model.fit <- stan(
file='model/eight-schools.stan',
data=schools_data,
iter=1000,
warmup=500,
chains=4,
seed=123456
)
NUTSの結果は下記。
Inference for Stan model: eight-schools.
4 chains, each with iter=1000; warmup=500; thin=1;
post-warmup draws per chain=500, total post-warmup draws=2000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu 8.0 0.2 4.7 -1.2 5.1 8.0 11.1 17.6 865 1
tau 6.6 0.3 5.9 0.3 2.4 5.2 8.9 21.9 455 1
eta[1] 0.4 0.0 1.0 -1.7 -0.3 0.4 1.0 2.2 1309 1
eta[2] 0.0 0.0 0.8 -1.7 -0.6 0.0 0.5 1.7 1431 1
eta[3] -0.2 0.0 1.0 -2.1 -0.9 -0.2 0.4 1.6 1294 1
eta[4] 0.0 0.0 0.9 -1.8 -0.6 0.0 0.5 1.7 1472 1
eta[5] -0.4 0.0 0.8 -1.9 -0.9 -0.4 0.2 1.3 1695 1
eta[6] -0.2 0.0 0.9 -1.9 -0.8 -0.2 0.4 1.5 1319 1
eta[7] 0.3 0.0 0.9 -1.5 -0.3 0.3 0.9 2.0 1185 1
eta[8] 0.1 0.0 0.9 -1.8 -0.5 0.1 0.7 2.0 1393 1
theta[1] 11.4 0.3 8.1 -1.7 6.0 10.3 15.6 31.0 872 1
theta[2] 7.9 0.1 5.9 -4.0 4.0 8.0 11.7 20.1 1851 1
theta[3] 6.0 0.3 8.1 -12.5 2.0 6.7 10.8 20.4 725 1
theta[4] 7.7 0.2 6.6 -6.5 3.6 7.9 11.6 21.4 1377 1
theta[5] 5.3 0.2 6.2 -9.0 1.6 5.7 9.5 16.5 1443 1
theta[6] 6.3 0.2 6.3 -7.6 2.5 6.6 10.5 17.7 1356 1
theta[7] 10.6 0.2 6.6 -0.8 6.2 9.9 14.4 26.1 1465 1
theta[8] 8.6 0.2 8.1 -8.0 4.4 8.5 12.7 25.6 1366 1
lp__ -4.8 0.1 2.6 -10.5 -6.4 -4.5 -2.9 -0.5 569 1
ADVI
続いて, ADVIで動かしてみる。
stan_model <- stan_model(file='model/eight-schools.stan')
model.fit <- vb(
stan_model,
data=schools_data,
output_samples=2000, # (iter - warmup) / thin * chains
seed=123456,
algorithm="meanfield"
)
ADVIの結果が下記。
Inference for Stan model: eight-schools.
1 chains, each with iter=2000; warmup=0; thin=1;
post-warmup draws per chain=2000, total post-warmup draws=2000.
mean sd 2.5% 25% 50% 75% 97.5%
mu 7.8 4.1 -0.4 5.1 7.6 10.5 15.7
tau 4.1 3.0 0.9 2.1 3.3 5.2 12.4
eta[1] 0.5 1.0 -1.6 -0.2 0.5 1.2 2.5
eta[2] 0.1 1.0 -1.8 -0.5 0.1 0.8 2.0
eta[3] -0.1 1.0 -2.1 -0.8 -0.1 0.6 1.9
eta[4] 0.1 0.9 -1.7 -0.5 0.1 0.7 1.9
eta[5] -0.3 0.9 -2.2 -0.9 -0.3 0.3 1.4
eta[6] -0.2 0.9 -2.0 -0.8 -0.1 0.4 1.7
eta[7] 0.3 0.9 -1.5 -0.3 0.3 1.0 2.2
eta[8] 0.1 1.0 -1.8 -0.6 0.1 0.7 2.0
theta[1] 9.8 6.8 -3.1 5.6 9.3 13.7 23.7
theta[2] 8.3 6.3 -4.3 4.5 8.1 12.0 21.7
theta[3] 7.2 6.7 -6.4 3.5 7.3 11.1 19.9
theta[4] 8.3 6.1 -3.9 4.7 8.1 11.9 20.1
theta[5] 6.5 6.0 -5.6 3.1 6.7 10.0 17.6
theta[6] 7.0 6.5 -5.9 3.4 7.1 10.7 18.9
theta[7] 9.1 6.2 -2.5 5.5 9.0 12.6 21.8
theta[8] 7.9 6.4 -5.0 4.2 8.0 11.5 20.4
lp__ 0.0 0.0 0.0 0.0 0.0 0.0 0.0
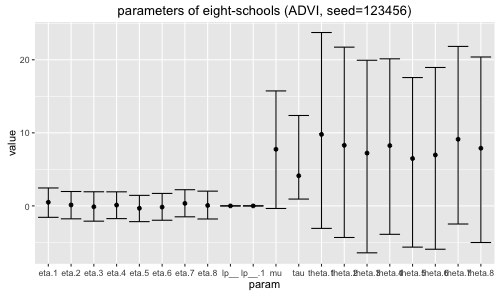
上記 (seed=123456) の mean と 95%ベイズ信頼区間 をプロットする。 (meadianの方が良かったかも)
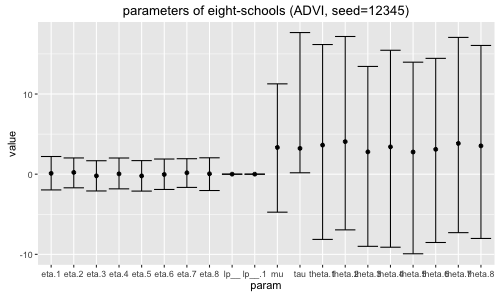
ADVIで seed を色々変えて初期値を変化させると, 結果が不安定になる。seed=12345の場合が下記で, 特に mu がイマイチな気が。
NIPS2015読み会の発表 [4]であったように, ADVIは初期値に敏感で局所最適解に陥りやすく, 初期値の設定に工夫が必要かも。
念のため Code は GitHub に置いた。
[1] Automatic Variational Inference in Stan
[2] 変分ベイズの自分向けの説明
[3] 変分近似(Variational Approximation)の基本(1) - 作って遊ぶ機械学習。
[4] "Automatic Variational Inference in Stan" NIPS2015_yomi2016-01-20