『入門 機械学習による異常検知―Rによる実践ガイド』を読了したので簡単なメモ。グラフが中心ですが Codeは GitHub にあります。
Rというかプログラミング知識に関しては, ほとんど必要しないと思いますが, 本書に掲載されている Codeは(紙面的な制約だと思いますが)部分的であるので少し注意が必要です。
私は初学者のため本記事の内容に間違いもあると思われます。見つけたら, ご指摘ください。
1. 異常検知の基本的な考え方
1.1 例題:健康診断
1.2 計算機に判定規則をつくらせたい
1.3 「確率分布」で正常パターンをつかむ
1.4 機械学習で確率分布を求める
1.5 やりたいことを具体的に整理する
1.6 異常の度合いを数値で表す
1.7 いろいろな手法を試してみる
機械学習で異常検知を行うとは, 異常or正常を区別するような知識を, 機械学習の手法を用いて過去のデータから計算機によって見つけ出させることを意味する。
正常のモデルを確率分布で定義して, それからのずれの度合いを異常度とする。この異常度にデータから閾値を求める。
正常モデル (確率分布)を構築する際に, 解く必要がある問題は下記に分類される。
- 密度推定問題
- 次元削減問題
- 回帰問題
- 分類問題
- 時系列解析問題
これらの問題を機械学習の手法を用いて解き, 異常度, 閾値を求めていく。
2. 正規分布に従うデータからの異常検知
2.1 異常検知手順の流れ
2.2 1 変数正規分布に基づく異常検知
2.2.1 ステップ1:分布推定
2.2.2 ステップ2:異常度の定義
2.2.3 ステップ3:閾値の設定
2.2.4 R での実行例
2.3 1 変数のホテリング理論の詳細*
2.3.1 1 変数正規分布の最尤推定
2.3.2 正規変数の和の確率分布(1次元)
2.3.3 標本分散の確率分布(1次元)
2.3.4 ホテリング統計量の確率分布(1次元)
2.4 多変量正規分布に基づく異常検知
2.4.1 ステップ1:多次元正規分布の最尤推定
2.4.2 ステップ2:異常度の定義
2.4.3 ステップ3:閾値の設定(ホテリングのT2 理論)
2.4.4 R での実行例
2.5 多変数のホテリング理論の詳細*
2.5.1 多変量正規変数の和の分布
2.5.2 多変量正規変数の平方和の分布
2.5.3 ホテリング統計量の分布
2.6 マハラノビス=タグチ法
2.6.1 手法の概要
2.6.2 R での実行例
2.6.3 QR 分解*
2.7 t 分布による異常判定*
2.8 ホテリング理論の課題
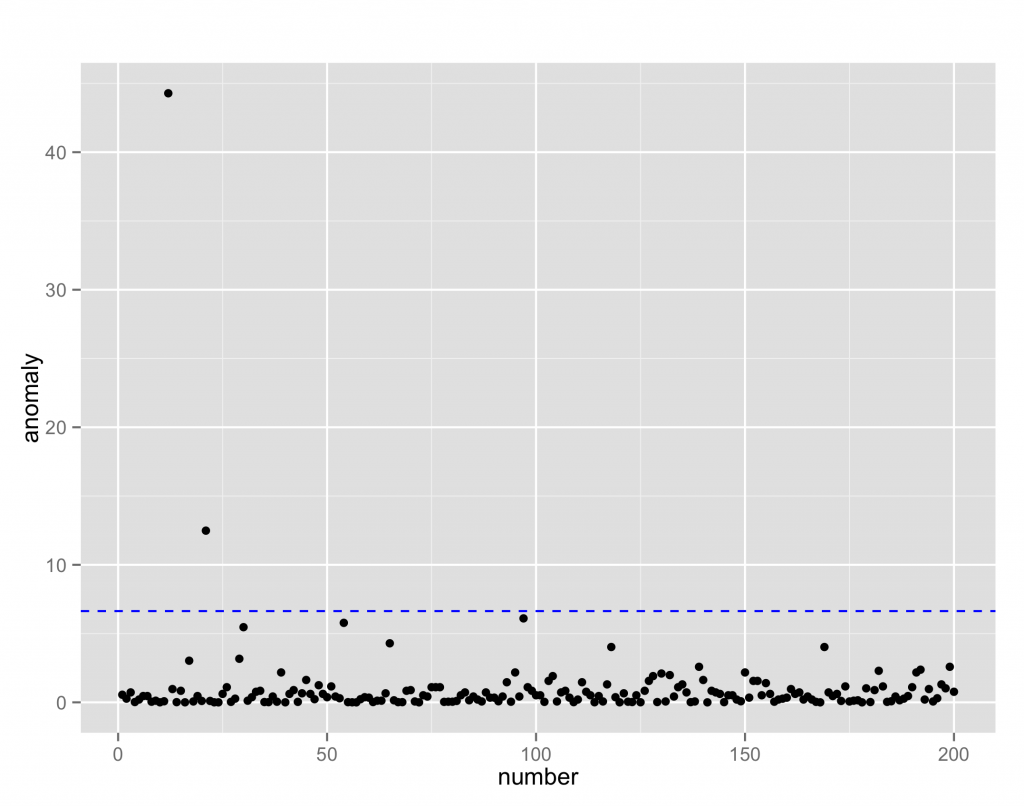
ホテリング理論は理論的な背景において, 統計学的な外れ値検出の理論がかなり部分を占めている。分布推定, 異常度計算, 閾値判定の順で行う。
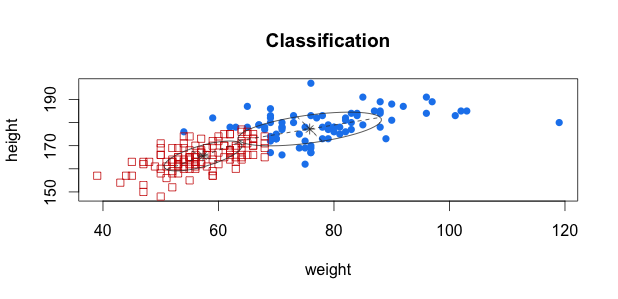
ホテリング理論による異常検知を試してみる。
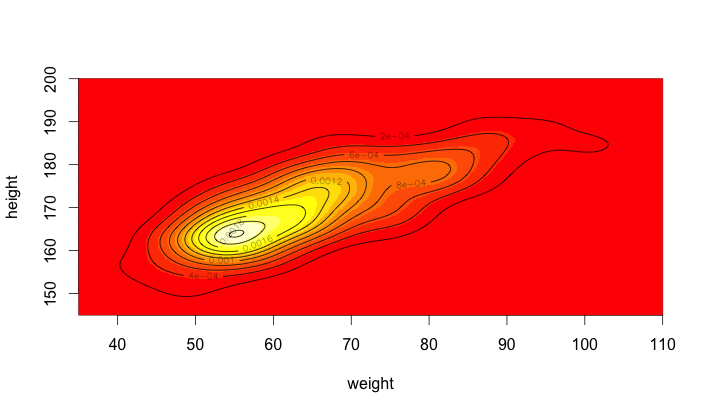
例題で用いるデータセットはDavisで, 200人の身長, 体重のデータ。
> help(Davis)
Davis {car} R Documentation
Self-Reports of Height and Weight
Description
The Davis data frame has 200 rows and 5 columns. The subjects were men and women engaged in regular exercise. There are some missing data.
Usage
Davis
Format
This data frame contains the following columns:
sex
A factor with levels: F, female; M, male.
weight
Measured weight in kg.
height
Measured height in cm.
repwt
Reported weight in kg.
repht
Reported height in cm.
閾値を1%としてカイ二乗分布から求める, Rではqchisq()を使う。
多変数の場合について。多変量について分布推定したことは、身長と体重なら2つの組み合わせについて正常パターンを学習したことに対応する。
最終的な結果は, 総合的な異常度となる。
本章ではマハラノビスタグチ法 (MTS)も紹介されている。
本章最後には, ホテリング理論の課題に触れられており, ホテリング理論は半導体プロセス制御に使われ理論が妥当なのは静的な値に留まる状況のみで動的に変化する系では適用が困難。
3. 非正規データからの異常検知
3.1 分布が左右対称でない場合
3.1.1 ガンマ分布の当てはめ
3.1.2 R での実行例
3.1.3 カイ二乗分布による異常度の当てはめ
3.2 訓練データに異常標本が混ざっている場合
3.2.1 正規分布の線形結合のモデル
3.2.2 期待値–最大化法:期待値ステップ
3.2.3 期待値–最大化法:最大化ステップ
3.2.4 R での実行例
3.3 分布がひと山にならない場合:近傍距離に基づく方法
3.3.1 k 近傍法
3.3.2 局所外れ値度
3.3.3 カーネル密度推定
3.3.4 R での実行例
3.4 分布がひと山にならない場合:クラスタリングに基づく方法
3.4.1 k 平均法
3.4.2 混合正規分布モデル
3.4.3 異常度の定義とR による実行例
3.5 期待値–最大化法の詳細*
3.5.1 イエンセンの不等式
3.5.2 最大化ステップ
3.6 支持ベクトルデータ記述法に基づく異常判定
3.6.1 データを囲む最小の球
3.6.2 R での実行例
2章では正常データが正規分布からの発生を仮定していたが, 3章では非正規データからの異常検知について。
使うデータセットは Davisで, {MASS} の fitdistr() によりパラメータを最尤推定で求める。
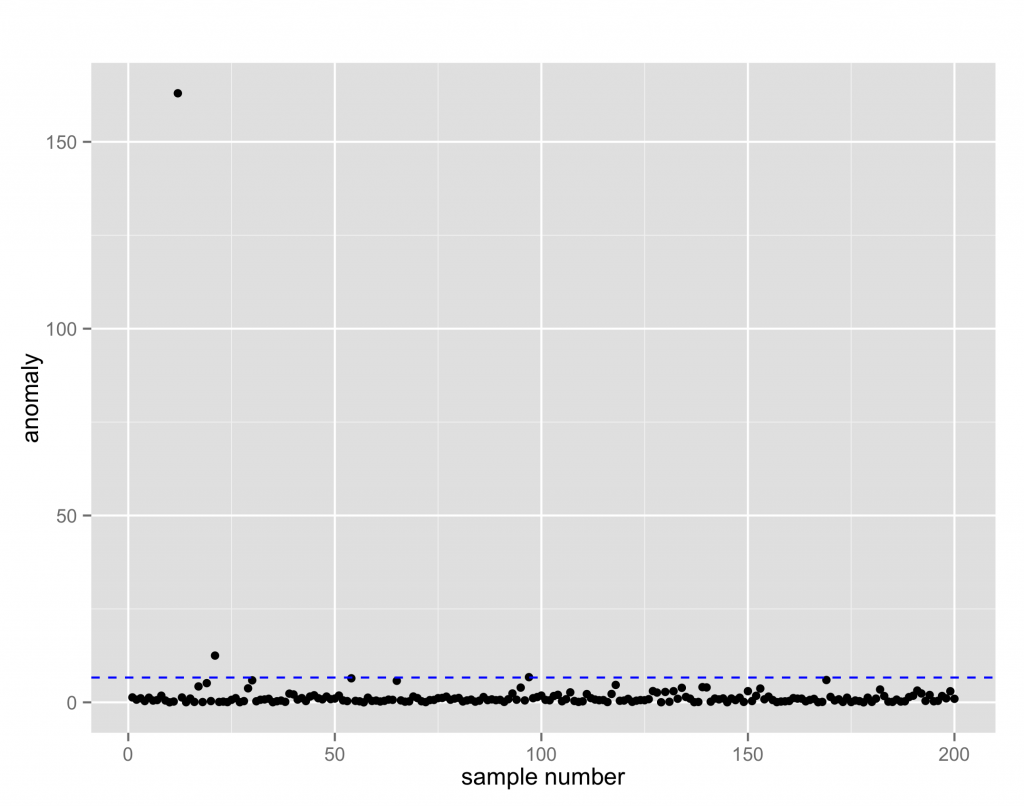
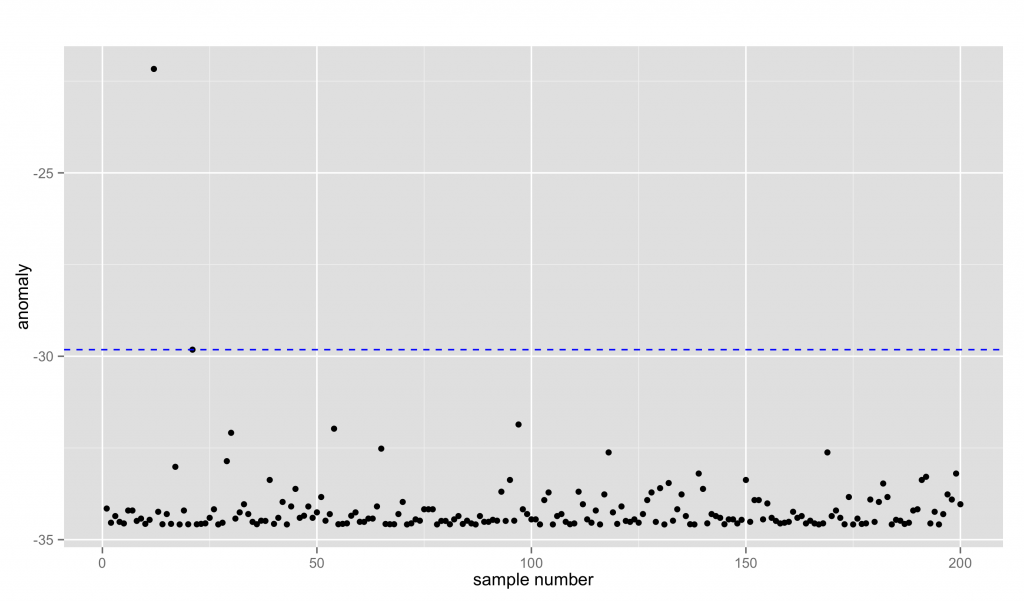
続いて, 正常信号に背景雑音が追加されるようなケースを考える。
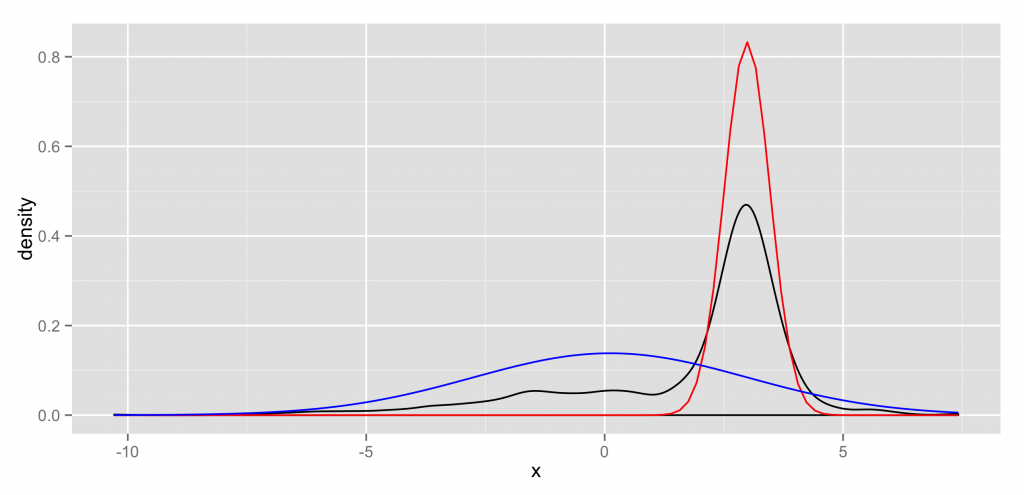
両方とも, 確率分布を正規分布とすると標本は2つの正規分布を線形結合した混合正規分布から発生したものとなる。
この場合, N(μ, σ)が2つ, さらに混合比(π0, π1)の計6つのパラメータを求めることになり最尤推定が難しくなるので, EM法 (Expextation Maximization)を使う。結果のグラフはblackが標本でred, blueが推定した2つの正規分布。
カーネル法を用いたカーネル密度推定を試してみる。
{KernSmooth}の dpik()により差し込み法によるバンド幅推定を行える。
k平均法によるクラスタリングを試してみる。{mclust}では, モデル選択にはBICを使っている。
他にも3章では, k近傍法, SVM (RBFカーネル)を紹介している。
4. 性能評価の方法
4. 性能評価の方法
4.1 基本的な考え方
4.2 正常標本精度と異常標本精度
4.2.1 正常標本に対する指標
4.2.2 異常標本に対する指標
4.3 異常検出能力の総合的な指標
4.3.1 分岐点精度とF 値
4.3.2 ROC 曲線の下部面積
4.4 モデルのよさの検証
4.4.1 モデル選択問題
4.4.2 交差確認法
4.4.3 赤池情報量規準とベイズ情報量規準
4.4.4 赤池情報量規準と平均対数尤度*
4.4.5 ベイズ情報量規準と周辺尤度*
異常検知能力は閾値設定によって変化する。また, 異常と呼ばれるくらいなので, 正常標本と異常標本の比には大きな差があることが多い。従って, 標本の割合が概ね釣り合っているとする一般的な2値分類問題に沿って考えると難しくなってしまう。
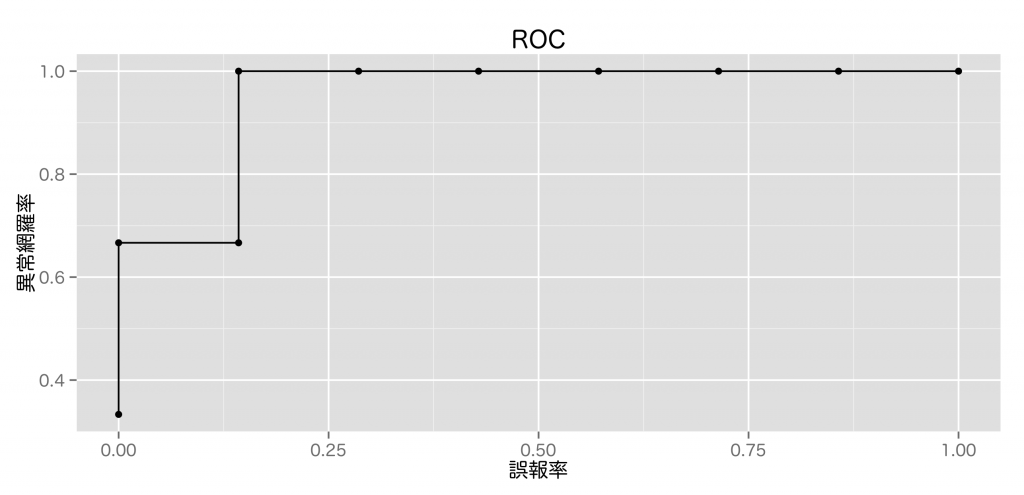
正常側, 異常側のどちらの視点に立つかで評価は変わってくる。前者は正常標本制度 (正答率), 後者は異常標本制度 (異常網羅率, リコール, ヒット率)となる。
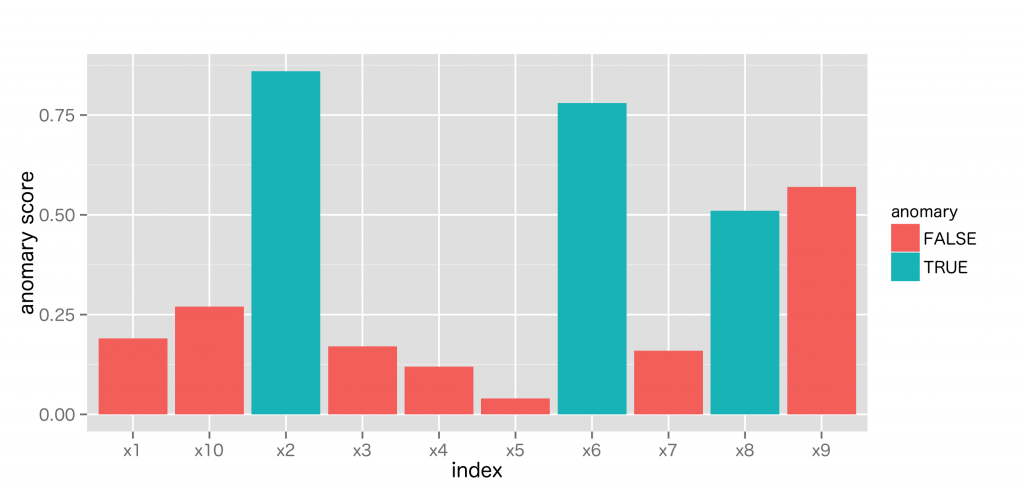
下記, 架空の異常度スコアの結果から性能評価を考える。
ROC曲線では評価の指標として, ROC曲線下面積 (area under the curve, AUC)が用いられる。
モデル選択手法としては交差確認法, AIC, BICが紹介されている。
5. 不要な次元を含むデータからの異常検知
5.1 次元削減による異常検知の考え方
5.2 主成分分析による正常部分空間の算出
5.2.1 分散最大化規準による正常部分空間
5.2.2 ノルム最大化規準による正常部分空間
5.2.3 二つの規準の等価性と特異値分解
5.3 主成分分析による異常検知
5.3.1 異常度の定義
5.3.2 ホテリングのT2 との関係
5.3.3 次元mの選択
5.3.4 R での実行例
5.4 確率的主成分分析による異常検知*
5.4.1 主成分分析の確率的モデル
5.4.2 平均ベクトルの推定
5.4.3 確率的主成分分析の期待値–最大化法
5.4.4 σ2 → 0 の極限と次元数m の決定
5.4.5 確率的主成分分析による異常度の定義
5.5 カーネル主成分分析による異常検知*
5.5.1 正常部分空間の算出
5.5.2 R での実行例
5.5.3 異常度の定義(m = 1)
5.5.4 異常度の定義(m > 1)
ホテリング理論は変数間の独立性を仮定しているので, 変数間に関係性がある場合, 共分散行列の逆行列が計算できなくてうまくいかない。
主成分分析によって, Dから標本の広がりを最もよく表現する正常部分空間 (主部分空間)を求めるアプローチを取る。正常部分空間からどの程度離れているかを異常度とする。
{MASS}に含まれるデータセット Cars93は名前の通り, 93種類の車種について価格や燃費などの27の特徴をまとめたデータ。
> help(Cars93)
Cars93 {MASS}
Data from 93 Cars on Sale in the USA in 1993
Description
The Cars93 data frame has 93 rows and 27 columns.
Usage
Cars93
Format
This data frame contains the following columns:
Manufacturer
Manufacturer.
Model
Model.
Type
Type: a factor with levels "Small", "Sporty", "Compact", "Midsize", "Large" and "Van".
Min.Price
Minimum Price (in \$1,000): price for a basic version.
Price
Midrange Price (in \$1,000): average of Min.Price and Max.Price.
Max.Price
Maximum Price (in \$1,000): price for “a premium version”.
MPG.city
City MPG (miles per US gallon by EPA rating).
MPG.highway
Highway MPG.
AirBags
Air Bags standard. Factor: none, driver only, or driver & passenger.
...
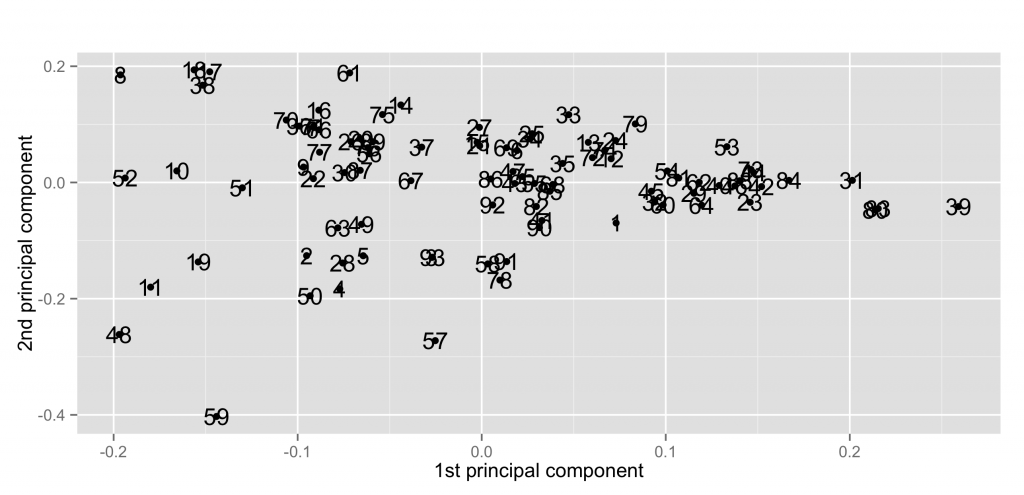
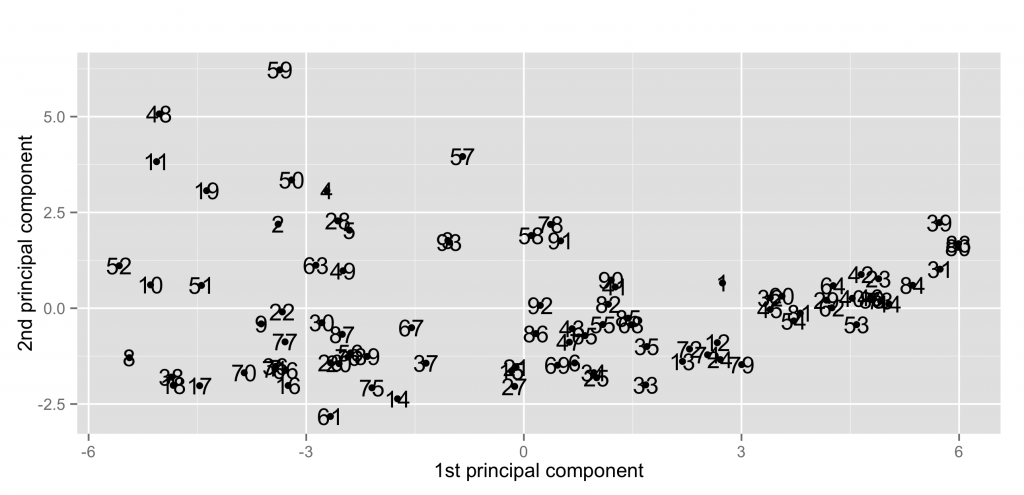
主成分分析による異常検知を試してみる。
続いて, カーネル主成分分析による異常検知。σ=0.01 では結果自体は似ている。
6. 入力と出力があるデータからの異常検知
6.1 入出力がある場合の異常検知の考え方
6.2 線形回帰モデルによる異常検知
6.2.1 問題の定義
6.2.2 最小二乗法としての最尤推定
6.2.3 異常度の定義
6.3 リッジ回帰モデルと異常検知
6.3.1 リッジ回帰の解
6.3.2 定数λの決定
6.3.3 異常度の定義
6.3.4 R での実行例
6.4 偏最小二乗法と統計的プロセス制御(1 次元出力)
6.4.1 問題の設定
6.4.2 正規直交基底による回帰モデルの変換
6.4.3 NIPALS 法(1 次元出力)
6.4.4 異常度の定義と異常検知手順
6.5 正準相関分析による異常検知
6.5.1 問題設定
6.5.2 一般化固有値問題としての正準相関分析
6.5.3 特異値分解による解と異常検知
6.6 ベイズ的線形回帰モデルと異常検知*
6.6.1 最大事後確率解としてのリッジ回帰
6.6.2 パラメターσ2 の決定
6.6.3 異常度の定義
入力と出力が組として与えられた場合の異常検知の考え方のひとつとして回帰問題 [1]を扱う。
最小二乗法による線形回帰には, 高次元になるほど似たような変数が出てきやすく, 逆行列の計算が不能になってしまいやすい問題 [2]がある。
この場合, リッジ回帰による解を使うことが推奨されるとのこと。
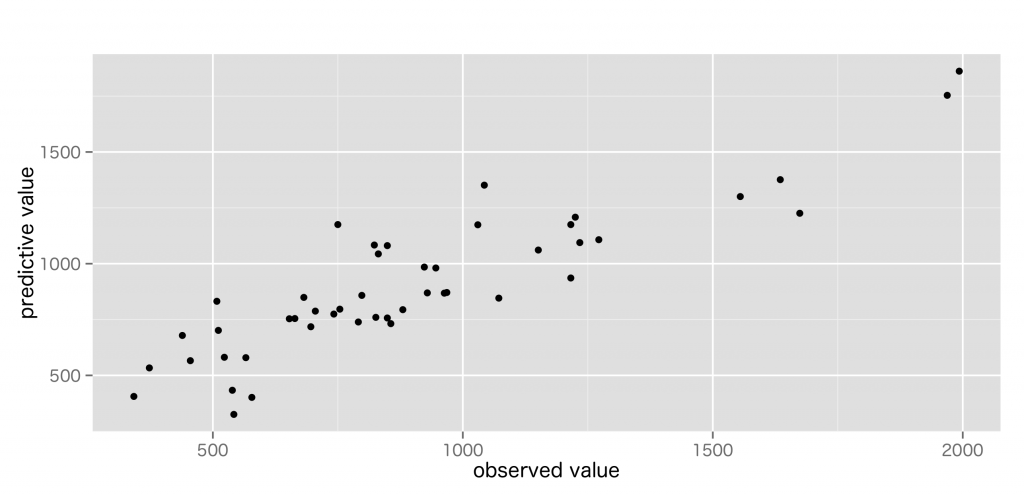
リッジ回帰による異常検知を試してみる。
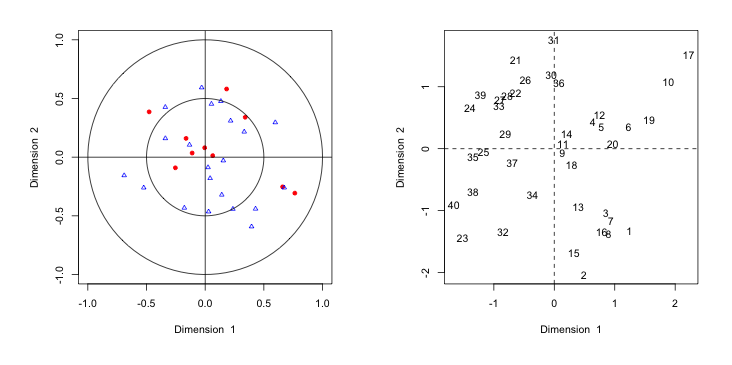
偏最小二乗法を多出力に拡張した, 正準相関分析による異常検知を試してみる。{CCA}の cc()を使う。
7. 時系列データの異常検知
7.1 近傍法による異常部位検出
7.1.1 スライド窓による時系列データの変換
7.1.2 異常部位検出問題
7.1.3 R での実行例
7.2 特異スペクトル変換法
7.2.1 特徴的なパターンの算出
7.2.2 変化度の定義
7.2.3 R での実行例
7.3 自己回帰モデルによる異常検知
7.3.1 1 変数の自己回帰モデル
7.3.2 ベクトル自己回帰モデル
7.3.3 次数r の決定
7.3.4 異常度の定義とR での実行例
7.4 状態空間モデルによる異常検知*
7.4.1 線形状態空間モデル
7.4.2 部分空間同定法:状態系列の推定
7.4.3 部分空間同定法:未知パラメターA, C,Q, R の推定
7.4.4 状態系列の逐次推定法:カルマンフィルタ
7.4.5 状態空間モデルを用いた異常検知
動的な系から生じる時系列データは, 観測値が互いに独立ではないので独立性を仮定する異常検知手法は使えない。
スライド窓により時系列データを, ベクトルの集まりに変換していくことで前章までの技術を使える。ただし, この操作により独立性を獲得したわけではない。
最近傍法を実装した{FNN}で異常部位検出を試してみる。ラグは履歴行列とテスト行列の相互位置を表す。
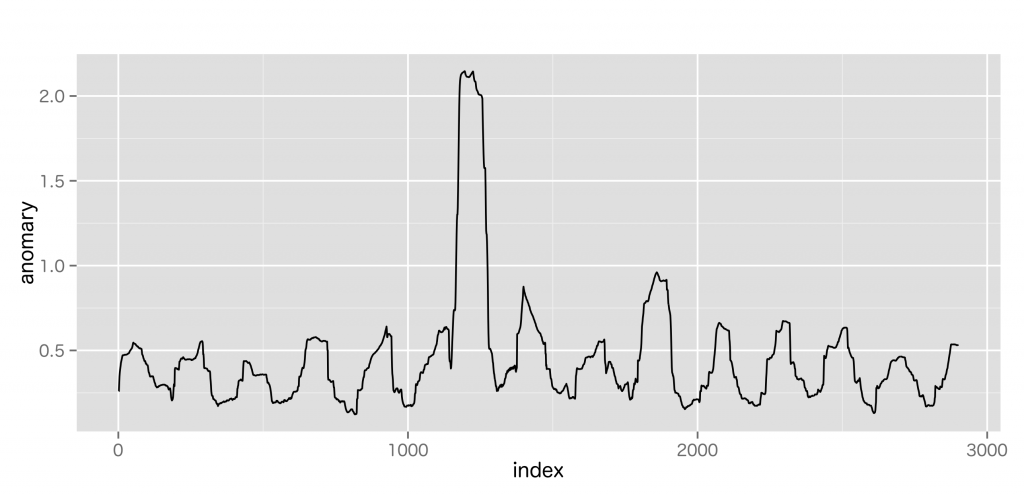
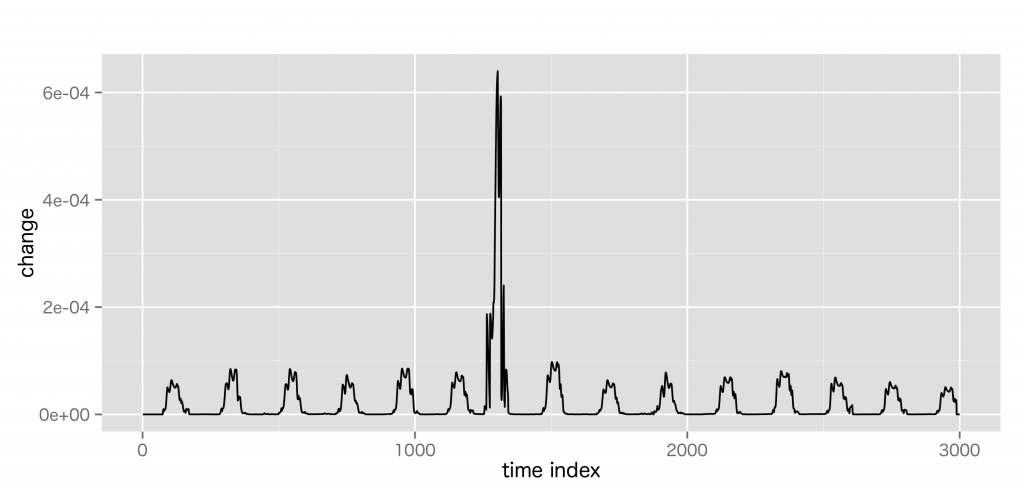
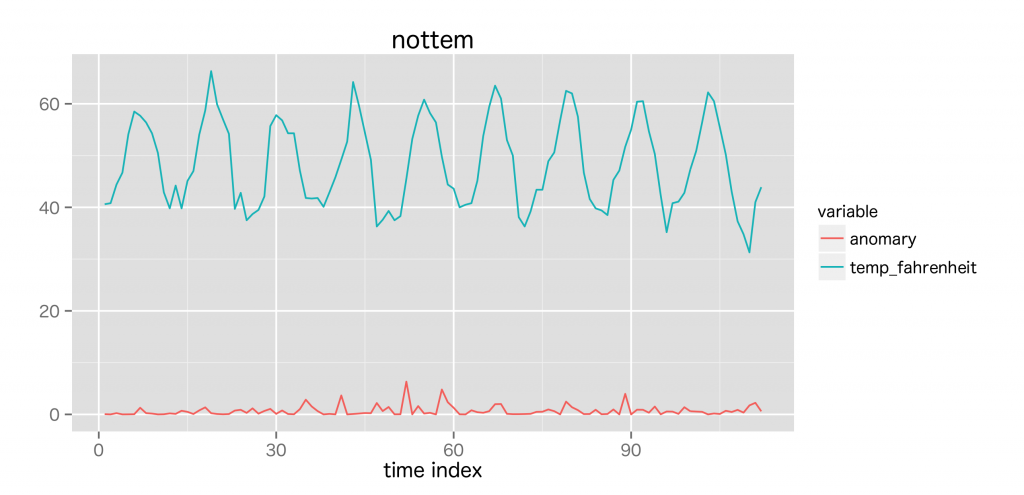
続いて, 時系列データの変化点を検出する手法。
特異スペクトル変換は, 今の状態は少し前の状態と似ているという仮定で, 特異値分解により時系列データの特徴パターンを求め, それに基づき変化度を求める。
心電図のようなスパイク状のデータでも安定して妥当な変化度を計算できる。ただし、特異値分解は比較的, 計算コストが大きい。
自己回帰 (AR)は過去のデータから, データ自身を予測する。正弦波のような波形には強いが, 心電図のようなスパイクデータには弱い。
自己回帰による異常検知を試してみる。時系列データの異常検知の評価には交差確認を適用しにくいため, AICが使われる。
また, 本章では状態空間モデルを用いた異常検知も紹介している。
8. よくある悩みとその対処法
8.1 数式を使いたくありません
8.2 モデルが変わってゆくのですが
8.3 変数の値の範囲が変で困っているのですが
8.3.1 ロジスティック変換
8.3.2 ボックス=コックス変換
8.4 正規分布の結果がおかしいのですが
8.5 データがベクトルになっていないのですが
8.6 異常の原因を診断したいのですが
8.7 分類問題にしてはいけませんか
8.8 さらに発展的な知識を得るために
統計的機械学習による異常検知に実際に取り組むにあたり, よく遭遇する問題とその対処法についての説明。
季節性によるモデルの変化への対処法や, 正規分布以外の分布に出くわした場合のロジスティック変換, ボックスコックス変換の使い方, 異常度だけでなく異常の原因を診断したいという難題に対しての考え方などが書かれている。
おわりに
本書を読む前からなんとなくは知っていた機械学習アルゴリズムがいくつかあったが, 異常検知の視点からみた時に新しい発見があったし, 理解も深まった気がするので読んでよかったと思います。個人的には特に異常検知をこれから学び始めたいひとにオススメです。
CodeはGitHubにあります。
[1] 入力xに対して出力yを予測するような問題。分類問題と並び, 統計的機械学習で重要な問題。
[2] 多重共線性