『みんなのR -データ分析と統計解析の新しい教科書-』を読了しました。 第19章 正則化と縮小 に関する私的メモを残しておきます。
ロジスティック回帰のモデル選択法の中で, Rでは Stepwise選択法 stats::step や Elastic Net {glmnet} など様々あります。今回はこの2つを試します。共通して使う DataSet は本書にも登場する American Community Survey (ACS)です。 ACSの FamilyIncodeが $15,000以上の record を True, それ以外を False とした目的変数 Income を作り, これを予測する回帰モデルをつくります。変数の数は14個で, 加えて特徴量を増やすため交互作用項も含めることにします。
正則化法の必要性
Stepwise選択法は伝統的なモデル選択の手法で, 偏F値 (Partial F Value)や AICを基準としてモデル選択を行う。
今回は, stats::step [1]で変数増減法を指定してAICが最小となるモデルを選択する。変数を増減させていく変数増減法以外にも, 変数増加法, 変数減少法を指定できる。
Stepwiseの初期値を説明変数が定数項のみから始めて, AICが下がらなくなるまで変数の増減を繰り返す。
require(coefplot)
d <- read.csv('data/acs_ny.csv', sep=',', header=TRUE, stringsAsFactors=FALSE)
d$Income <- with(d, FamilyIncome >= 150000)
acs <- d[,c(-1,-2,-3,-13)]
null.model <- glm(
cbind(Income, 2 - Income) ~ 1,
data=acs,
family=binomial(link=logit)
)
full.model <- glm(
cbind(Income, 2 - Income) ~ NumBedrooms + NumChildren + NumPeople +
NumRooms + NumUnits + NumVehicles + NumWorkers + OwnRent + YearBuilt +
ElectricBill + FoodStamp + HeatingFuel + Insurance + Language,
data=acs,
family=binomial(link=logit)
)
model.step <- step(null.model, scope=list(lower=null.model, upper=full.model), direction='both')
exp(model.step$coefficients)
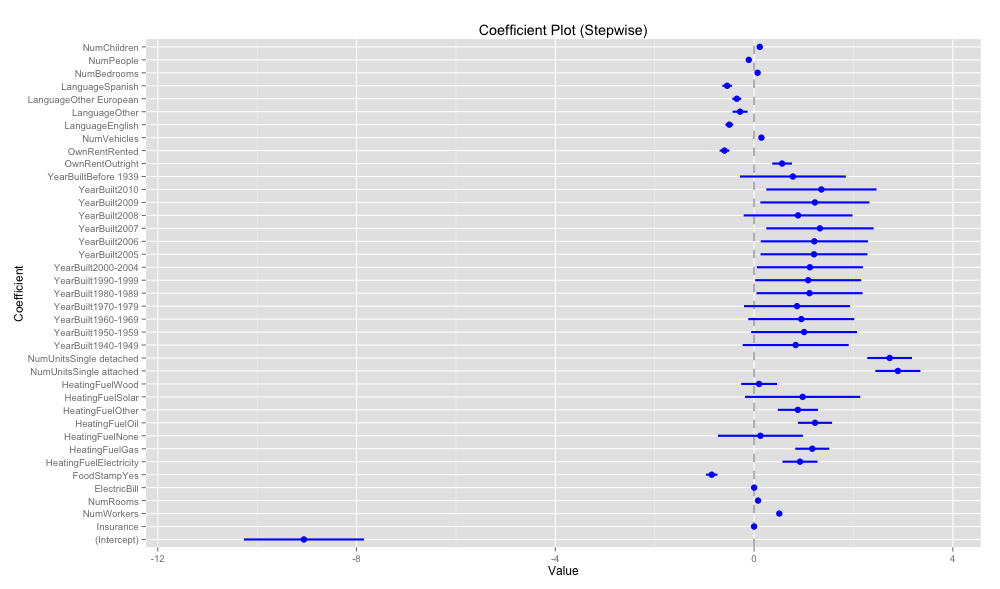
coefplot.default(model.step, title='Coefficient Plot (Stepwise)')
選択されたモデルが下記となった。
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -9.060e+00 1.208e+00 -7.499 6.44e-14 ***
NumBedrooms 7.114e-02 1.762e-02 4.038 5.40e-05 ***
NumChildren 1.142e-01 2.160e-02 5.289 1.23e-07 ***
NumPeople -1.069e-01 1.982e-02 -5.392 6.96e-08 ***
NumRooms 7.999e-02 7.362e-03 10.866 < 2e-16 ***
NumUnitsSingle attached 2.894e+00 4.525e-01 6.396 1.59e-10 ***
NumUnitsSingle detached 2.728e+00 4.493e-01 6.073 1.26e-09 ***
NumVehicles 1.477e-01 1.958e-02 7.542 4.62e-14 ***
NumWorkers 5.074e-01 2.626e-02 19.319 < 2e-16 ***
OwnRentOutright 5.634e-01 1.987e-01 2.836 0.004575 **
OwnRentRented -5.955e-01 9.893e-02 -6.020 1.75e-09 ***
YearBuilt1940-1949 8.378e-01 1.067e+00 0.785 0.432374
YearBuilt1950-1959 1.007e+00 1.066e+00 0.945 0.344812
YearBuilt1960-1969 9.501e-01 1.066e+00 0.891 0.372894
YearBuilt1970-1979 8.637e-01 1.067e+00 0.810 0.418070
YearBuilt1980-1989 1.115e+00 1.067e+00 1.046 0.295768
YearBuilt1990-1999 1.089e+00 1.067e+00 1.021 0.307233
YearBuilt2000-2004 1.123e+00 1.068e+00 1.052 0.292682
YearBuilt2005 1.206e+00 1.076e+00 1.121 0.262394
YearBuilt2006 1.213e+00 1.078e+00 1.124 0.260808
YearBuilt2007 1.325e+00 1.080e+00 1.227 0.219869
YearBuilt2008 8.853e-01 1.096e+00 0.808 0.419188
YearBuilt2009 1.223e+00 1.098e+00 1.114 0.265089
YearBuilt2010 1.355e+00 1.109e+00 1.221 0.222049
YearBuiltBefore 1939 7.805e-01 1.066e+00 0.732 0.463939
ElectricBill 1.712e-03 1.498e-04 11.424 < 2e-16 ***
FoodStampYes -8.526e-01 1.146e-01 -7.442 9.94e-14 ***
HeatingFuelElectricity 9.239e-01 3.523e-01 2.623 0.008726 **
HeatingFuelGas 1.171e+00 3.422e-01 3.423 0.000619 ***
HeatingFuelNone 1.285e-01 8.548e-01 0.150 0.880498
HeatingFuelOil 1.227e+00 3.428e-01 3.579 0.000346 ***
HeatingFuelOther 8.815e-01 4.047e-01 2.178 0.029384 *
HeatingFuelSolar 9.772e-01 1.160e+00 0.842 0.399555
HeatingFuelWood 1.015e-01 3.607e-01 0.281 0.778328
Insurance 3.122e-04 1.388e-05 22.490 < 2e-16 ***
LanguageEnglish -4.980e-01 7.865e-02 -6.333 2.41e-10 ***
LanguageOther -2.816e-01 1.507e-01 -1.869 0.061681 .
LanguageOther European -3.480e-01 8.992e-02 -3.870 0.000109 ***
LanguageSpanish -5.420e-01 9.704e-02 -5.586 2.33e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 16989 on 22744 degrees of freedom
Residual deviance: 13554 on 22706 degrees of freedom
AIC: 19960
{coefplot}の coefplotで係数パラメータをplotする。
p値の高い変数も残っていて, あまり変数の数が絞り込まれていない気がする。
日本統計学会誌. 第 39 巻 回帰モデリングとL1 型正則化法の最近の展開 によると, Stepwiseによる変数増減法では高次元小標本データ (p >> n) に対しては最適な変数を選ぶとは限らず不安定になることがあるようだ。そのまま引用すると,
高次元小標本データに対して変数選択問題を考える場合,総当たり法では計算時間的に困難となり,変数増減法では最適な変数を選ぶとは限らず不安定になることが報告されている (Breiman (1996)).
そこで,推定と変数選択を同時に行うことができる lasso は,高次元小標本データに対する変数選択を行う上で有用な手法である.
このような高次元小標本データあるいは多重共線性のある状況では最小二乗推定量が存在しない (逆行列が求まらない) 場合があり正則化法が必要となる。
Lasso
Lasso (L1正則化項, L1ノルム) は正則化法のひとつで,モデルの変数選択と次元削減を同時に行う。線形回帰モデルに対しては, 制約式の性質からパラメータの一部を完全に 0 と推定する特徴がある。 Lasso はスパース化において強力な手法である。
しかし, 上記引用文は下記のように続いている。
しかし,“p > n”の場合 lasso は高々 n 個の変数までしか選択できないことが知られている (Efron et al. (2004),
Rosset et al. (2004)).また,遺伝子データのような説明変数間に高い相関性を有しているデータの変数選択を考えるとき,lasso ではこの相関を捉えきれず適切な変数選択が行われるとは限らないことが知られている.
上記の問題点の解決策のひとつとして, Elastic Netがある。[2]
Elastic Net
Elastic Net は過学習や多次元化に対する, 正則化と係数縮小の手法である。
本書 (みんなのR) からElastic Netの式を引用する。
ここで正則化項は以下となる。
p > n で非ゼロパラメータが高々 n 個までしか選択されない Lasso の問題は, 上記のように正則化項が L1 正則項と L2 正則項の線形結合となっているので, 0 ≤ α ≤ 1 の範囲で Lasso と Ridge を比率的に混合できることから Ridge の比率を高めることで緩和できる。
また, Lasso では相関が高い変数群があると中から1つしか選択されないが Elastic Net では Grouping effect (Zou and Hastie, 2005) により解決されている。
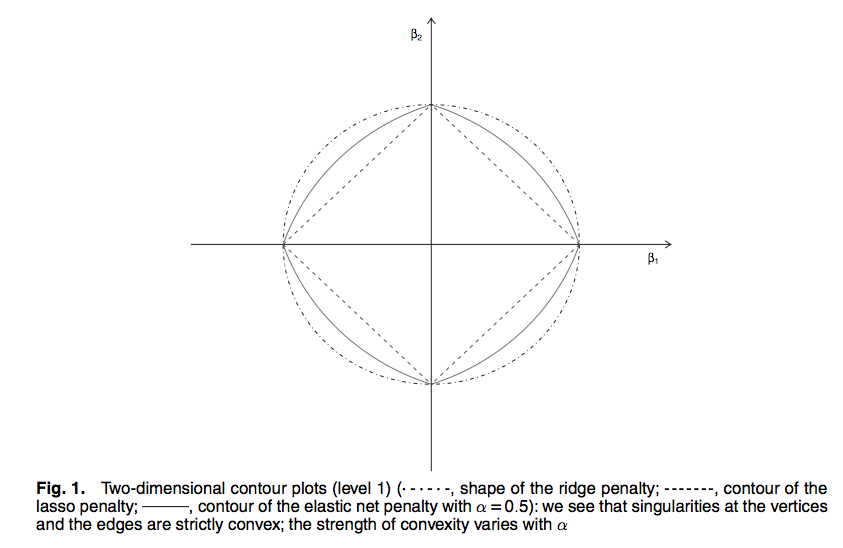
元論文 [2]から引用した以下の図で Lasso と Ridge の関係をみてみる。
図中の係数パラメータの二次元プロットで, ダイヤモンド形が Lasso, 円形が Ridge の場合の制約領域 (ノルム制約集合) を表す。
(図中にはないが) 損失を最小化する項が表す等高線を描く楕円の最小値は最小二乗推定量 (OLS) となる。この楕円を広げていき制約領域に接する点が正則化法で得られる推定値となる。 制約領域の形から Ridge が係数パラメータの推定値を 0 へと縮小するのに対して, Lasso は楕円が角に接しやすいことから係数パラメータを完全に 0 とするという違いがあることが図からイメージできる。ただし, Lasso でも正則化パラメータ λ によっては角に当たらないこともよくある。
glmnet
Elastic NetのR実装は 論文の著者自身が開発した {glmnet} がある。
glmnetの準備として matrix型の予測因子行列を必要とするので, model.matrix で デザイン行列 を得られるが, factor の扱いに関しては useful::build.x を使うと簡単に出来る。
acs <- read.csv('data/acs_ny.csv', sep=',', header=TRUE, stringsAsFactors=FALSE)
acs$Income <- with(acs, FamilyIncome >= 150000)
acsX <- build.x(
Income ~ NumBedrooms + NumChildren + NumPeople + NumRooms + NumUnits +
NumVehicles + NumWorkers + OwnRent + YearBuilt + HouseCosts +
ElectricBill + FoodStamp + HeatingFuel + Insurance + Language - 1,
data=acs, contrasts=FALSE
)
acsY <- build.y(
Income ~ NumBedrooms + NumChildren + NumPeople + NumRooms + NumUnits +
NumVehicles + NumWorkers + OwnRent + YearBuilt + HouseCosts +
ElectricBill + FoodStamp + HeatingFuel + Insurance + Language - 1,
data=acs
)
glmnetで Lasso回帰
glmnetでは 正則化パラメータ α を指定する。特に α=1の時を Lasso回帰, α=0の時を Ridge回帰と呼ぶ。それぞれに用いられている正則化項をL1ノルム, L2ノルムと呼ぶ。
# Cross Validation - Lasso
acs.cv1 <- cv.glmnet(x=acsX, y=acsY, family='binomial', nfold=5, alpha=1)
acs.cv1$lambda.min
acs.cv1$lambda.1se # one standard deviation
plot(acs.cv1, main='Lasso alpha=1.0')
coef(acs.cv1, s='lambda.1se') # var selection
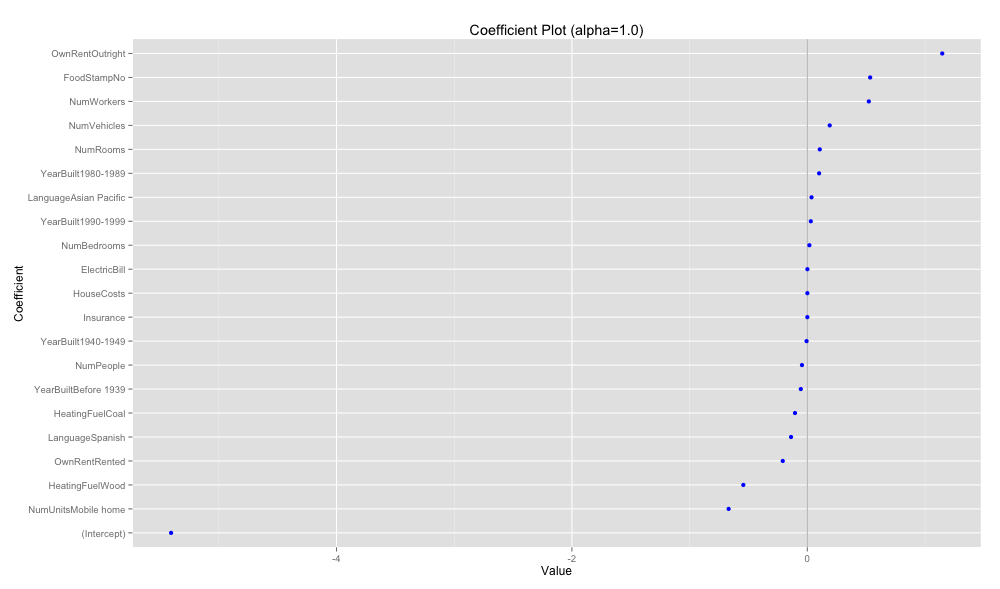
coefplot(acs.cv1, 'Coefficient Plot (alpha=1.0)')
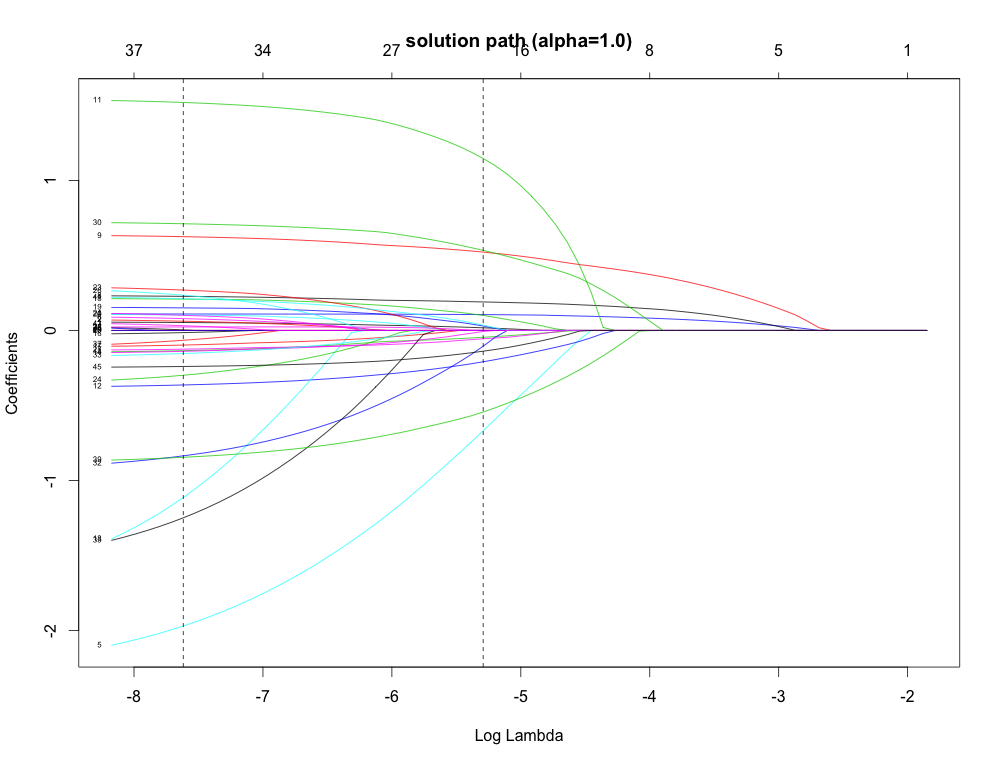
plot(acs.cv1$glmnet.fit, xvar='lambda')
abline(v=log(c(acs.cv1$lambda.min, acs.cv1$lambda.1se)), lty=2)
下記では完全に 0 と推定された変数は除かれている。
正則化パラメータを動かした時の最適化問題の軌跡である Solution path (Regularization path) を図示する。左の点線が lambda.min で最小平均 cross-validated error, 右の点線が lambda.1se (one-σ)で最小の1標準誤差となる 正則化パラメータ λ の値。one-σ の方がより自由度を節約できる。
β は変数間の相関がある場合では 0 になった後に, 再度出現したりすることもあるようだ。
glmnetで Ridge回帰
Ridge [Horel and Kennard, 1970] はモデルの係数パラメータの二乗和を正則化項とした正則化手法で, 安定した予測精度を出すために係数パラメータを縮小する。
# Cross Validation - Ridge
acs.cv2 <- cv.glmnet(x=acsX, y=acsY, family='binomial', nfold=5, alpha=0)
acs.cv2$lambda.min
acs.cv2$lambda.1se # one standard deviation
plot(acs.cv2, main='Ridge (alpha=0.0)')
coef(acs.cv2, s='lambda.1se')
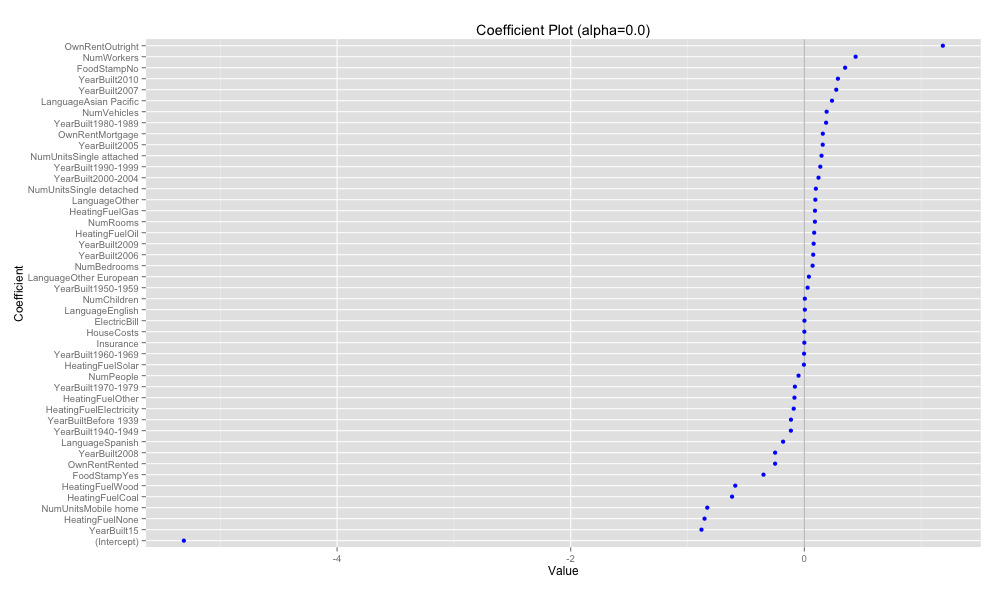
coefplot(acs.cv2, 'Coefficient Plot (alpha=0.0)')
plot(acs.cv2$glmnet.fit, xvar='lambda')
abline(v=log(c(acs.cv2$lambda.min, acs.cv2$lambda.1se)), lty=2)
正則化パラメータの選択
Elasctic Net では正則化パラメータとして縮小量を制御, つまり正則化項を重視する度合いを決める全体的なパラメータ λ と Lassoと Ridge の混合比率を決める α がある。正則化パラメータ λ の値に依存して様々なモデルが構成されるので λ の選択はひとつのポイントとなる。
適切な λの選択手法のひとつとして, 交差検証 (Cross Validation; CV) [3]がある。glmnetでは 既に上記で使っている cv.glmnetで 自動的に交差検証を行うことができ, 異なる λ を用いて Solution pathを適合させる。安定した交差検証手法としては K-fold CV が良く用いられる。λ=0 は罰則なしとなり, λ=∞ で全ての係数の推定値が 0 となる。
また, 適切な α を選択する方法として α を細かく変動させて標準誤差が最小となる α を探索する方法を取る。SVM のグリッドサーチのような感じ。
cv.glmnet 自体は並列実行可能なので, foreachで α をずらしながら標準誤差を計算していく。並列実行のために {parallel}, {doParallel} を使う。
# range of search
theFolds <- sample(rep(x=1:5, length.out=nrow(acsX)))
alphas <- seq(from=0.5, to=1, by=0.05)
cluster <- makeCluster(2)
registerDoParallel(cluster)
before <- Sys.time()
acsDouble <- foreach(i=1:length(alphas),
.errorhandling='remove',
.inorder=FALSE,
.multicombine=TRUE,
.export=c('acsX', 'acsY', 'alphas', 'theFolds'),
.packages='glmnet') %dopar% {
print(alphas[i])
acs.cv1 <- cv.glmnet(x=acsX, y=acsY, family='binomial', nfold=5, foldid=theFolds, alpha=alphas[i])
}
after <- Sys.time()
after - before
# Time difference of 1.563828 mins
stopCluster(cluster)
sapply(acsDouble, class)
extractGlmnetInfo <- function(obj) {
lambda.min <- obj$lambda.min
lambda.1se <- obj$lambda.1se
which.min <- which(obj$lambda == lambda.min)
which.1se <- which(obj$lambda == lambda.1se)
data.frame(
lambda.min=lambda.min,
error.min=obj$cvm[which.min],
lambda.1se=lambda.1se,
error.1se=obj$cvm[which.1se]
)
}
# lapply for list
alphaInfo <- Reduce(rbind, lapply(acsDouble, extractGlmnetInfo))
alphaInfo$Alpha <- alphas
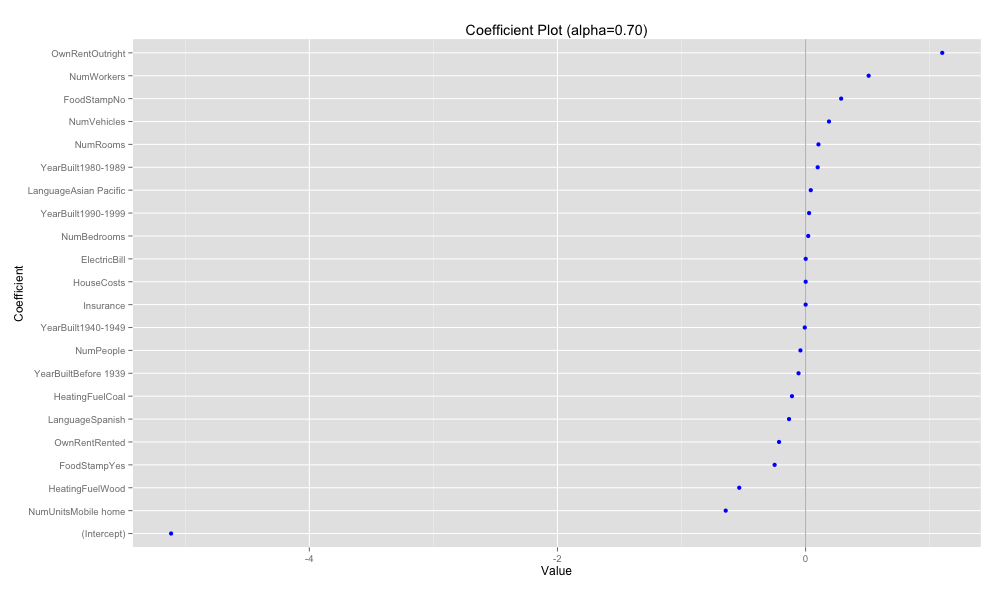
error.1seが最小になったのが α=0.70となった。
> alphaInfo
lambda.min error.min lambda.1se error.1se Alpha
1 0.0008165096 0.7749260 0.009172048 0.7801316 0.50
2 0.0008146529 0.7749227 0.008338226 0.7799511 0.55
3 0.0007467652 0.7749201 0.007643373 0.7798048 0.60
4 0.0006893217 0.7749181 0.007055422 0.7796840 0.65
5 0.0006400845 0.7749165 0.006551463 0.7795832 0.70
6 0.0006556591 0.7749148 0.006710874 0.7802125 0.75
7 0.0006146804 0.7749133 0.006291445 0.7801291 0.80
8 0.0005785227 0.7749121 0.005921360 0.7800569 0.85
9 0.0005463826 0.7749110 0.005592395 0.7799939 0.90
10 0.0005176256 0.7749102 0.005298059 0.7799386 0.95
11 0.0004917443 0.7749094 0.005033156 0.7798906 1.00
α=0.70でglmnetを再度実行する。
# Cross Validation - min 1se (alpha=0.70)
acs.cv3 <- cv.glmnet(x=acsX, y=acsY, family='binomial', nfold=5, alpha=0.70)
acs.cv3$lambda.min
acs.cv3$lambda.1se # one standard deviation
plot(acs.cv3, main='alpha=0.70')
coef(acs.cv3, s='lambda.1se')
coefplot(acs.cv3, 'Coefficient Plot (alpha=0.70)')
plot(acs.cv3$glmnet.fit, xvar='lambda')
abline(v=log(c(acs.cv3$lambda.min, acs.cv3$lambda.1se)), lty=2)
p >> n ではデータ分割 (k-fold) に偏りが生じて CV で安定的に良い正則化パラメータを得るのが難しいという話もあり, stability selection (meinshausen and buhlmann, 2010) という手法が用いられることもあるようである。
Lassoの発展として正則化項をグループ化する Group Lasso [5] がある。また, L1正則化に関連するモデル選択手法として FDR (False Discovery Rate)を制御しながら, Lasso で変数選択を行う Knockoff procedure [6]という方法もあったり, 現在も研究が続けられている。
他にもスパース推定に関して調べると FOBOS, DAL, ADMM [7], 圧縮センシングとか初めて聞く単語が出てきてちょっと腰が引ける。
スパース性に基づく機械学習 (2015/12/22 追記)
正則化に関して『 スパース性に基づく機械学習 (機械学習プロフェッショナルシリーズ) 』がオススメです。特に3章 スパース性の導入 では L1正則化によりスパース性が得られる説明がとてもわかり易く解説されていると思います。人工データを用いた Largest-K などによるテスト誤差の比較もあり素晴らしかったです。また, Elastic Net は 9章 重複型スパース正則化 に書かれています。
[1] AICを使った変数選択
[2] Regularization and variable selection via the elastic net [Zou, Hui; Hastie, Trevor 2005]
[3] Cross-validation (CV) はモデルの汎化性を検証するためにサンプル集合から汎化誤差を推定する方法。out-of-sample testing とも呼ばれる。
[4] スパース推定
[5] Group Lassoでグループごと重みが0に潰れる理由
[6] 機械学習サマースクール2015@京都大学に行ってきました!
[7] 正則化学習法における最適化手法
[8] Glmnet Vignette
[9] Sparsity and the Lasso
[10] Lassoタイプの正則化法に基づくスパース推定法を用いた 超高次元データ解析
[11] スパース推定概観:モデル・理論・応用