Machine Learning – ページ 21

『Python機械学習プログラミング達人データサイエンティストによる理論と実践』第3章分類問題の 3.6 決定木学習に関連した内容です。

決定木をサポートしたライブラリは R だと {rpart} パッケージ, Pythonだと scikit-learn を初めとして数多くあります。当初は Go で書いてみようと思ったのだけど, その前にまず Python で書いてみようということで始めたら意外と時間を使ってしまったので Go は次回に回したいと思います。

なので今回の内容は, scikit-learn の DecisionTreeClassifier の Iris データに対しての分類器と同様の分類器を得る Python コードを書いてみる所までになります。

決定木

決定木は意味解釈可能性 (Interpretability) に配慮されたモデルで, 機械学習アルゴリズムの中でも事前の標準化を必要としないアルゴリズム。情報利得が最大となる特徴量でデータを分割していくのを再帰的に行う。
特徴空間を矩形に分割するため複雑な決定境界を構築できる反面, 木が深くなるほど決定境界は複雑となり過学習に陥り易い。そのため, 木の深さを制限する剪定 (prune) を行い過学習を抑制する。剪定には決定木の成長中に剪定を行う事前剪定 (pre-pruning) と, 決定木の構築後に剪定を行う事後剪定 (post-pruning) がある。また, 単一の決定木と比べると決定木の並列アンサンブルであるランダムフォレスト (Random Forest; RF) は汎化性能に優れる。

目的関数

最も情報利得の高い特徴量でノードを分割するための目的関数を定義する。二分決定木の場合は以下となる。

$\begin{eqnarray*} IG ( D_{p}, f ) = I(D_{p}) - \frac {N_{left}} {N_{p}} I(D_{left}) - \frac {N_{right}} {N_{p}} I(D_{right}) \end{eqnarray*}$

f は特徴量, Dpは親データセット, Dleft, Drightは子ノード。Iは不純度で, ノードに含まれるサンプルの異なったクラスの割合の程度。

分割条件

分類問題でよく使われる分割条件は以下がある。回帰問題に対しては MSE (Mean Squared Error) などが使われる。

エントロピー (entropy)
ジニ不純度 (gini impurity)
分類誤差 (classification error)

エントロピー

エントロピーは相互情報量が最大化するように試みる条件である。ノード t でクラス i に属するサンプルの割合を p(i|t) とする。また, 取り得るクラス数を c とする。
ノード t 内でサンプルが全て同じクラス i に属している場合は, エントロピーは 0 となる。逆に各クラスが一様に分布している場合は最大になる。

$\begin{eqnarray*} I_{H} (t) = - \sum_{i=1}^{c} p (i|t) \log_{2} p (i|t) \end{eqnarray*}$

def _entropy(self, target, classes):
        n = target.shape[0]
        entropy = 0.0
        for c in classes:
            p = len(target[target == c]) / n
            if p > 0.0:
                entropy -= p * np.log2(p)
        return entropy

ジニ不純度

エントロピーと同様に誤分類を最小化する条件である。不純度 I はノード t に含まれるサンプルが全て異なるクラスの場合に最も高くなり, サンプルが全て同じクラスの場合 0 となる。

$\begin{eqnarray*} I_{G} (t) = 1 - \sum_{i=1}^{c} p (i|t)^2 \end{eqnarray*}$

def _gini(self, target, classes):
        n = target.shape[0]
        return 1.0 - sum([(len(target[target == c]) / n) ** 2 for c in classes])

例えば, [“犬”, “犬”, “犬”, “猫”, “猫”] の場合, ジニ不純度は 1-(3/5)^2-(2/5)^2 = 0.48 となる。より犬の比率が高い [“犬”, “犬”, “犬”, “犬”, “猫”] の場合では 1-(4/5)^2-(1/5)^2 = 0.32 となり, 後者の方が不純度は低い。この例をコードで確認してみる。

$ ipython
Python 3.6.8 |Anaconda, Inc.| (default, Dec 29 2018, 19:04:46)

In [1]: def _gini(target, classes):
   ...:         n = target.shape[0]
   ...:         return 1.0 - sum([(len(target[target == c]) / n) ** 2 for c in classes])
   ...:

In [2]: import numpy as np

In [3]: target = np.array(["dog", "dog", "dog", "cat", "cat"])

In [4]: classes = np.unique(target)

In [5]: _gini(target, classes)
Out[5]: 0.48

In [6]: target = np.array(["dog", "dog", "dog", "dog", "cat"])

In [7]: _gini(target, classes)
Out[7]: 0.31999999999999984

分類誤差

分類誤差はノード t のクラス確率の変化にあまり敏感でないため, 決定木を成長させるのにあまり適していない。

$\begin{eqnarray*} I_{E} (t) = 1 - \max \{ p (i|t) \} \end{eqnarray*}$

def _classification_error(self, target, classes):
        n = target.shape[0]
        return 1.0 - max([len(target[target == c]) / n for c in classes])

scikit-learn

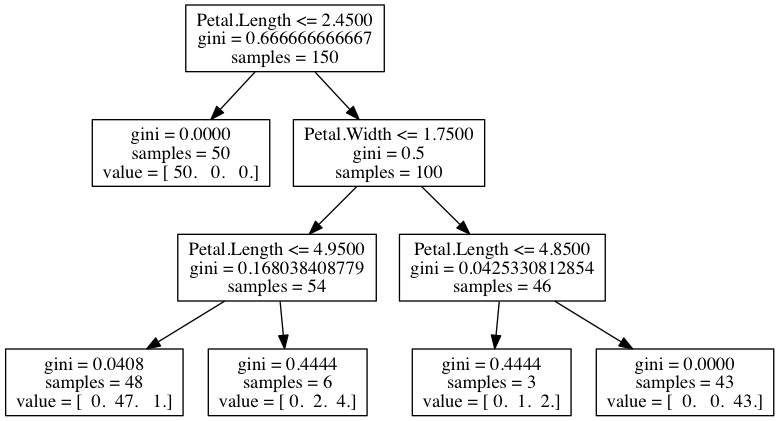
本書でも登場する scikit-learn の DecisionTreeClassifier クラスによる Iris に対する多クラス分類と, 木の可視化の例。

# -*- coding: utf-8 -*-

from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.externals.six import StringIO
from sklearn.tree import export_graphviz

def save_tree(tree):
    dot_data = StringIO()
    export_graphviz(tree, out_file='tree.dot',
        feature_names=["Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width"])


if __name__ == "__main__":
    iris = load_iris()

    dt = DecisionTreeClassifier(max_depth=3)
    dt = dt.fit(iris.data, iris.target)

    save_tree(dt)

dotファイルを png に変換する。

$ dot -Tpng tree.dot -o img/tree.png

得られた決定木と同様の決定木分類器を得るためのコードを書いてみる。

決定木分類器を Python で書いている

Code は GitHub に置いた。

Treeクラスの build() で情報利得を最大化するような特徴と分割閾値を探索し, 分割できなくなるまで再帰的に分割する。
分割条件は先ほど挙げた, エントロピー, ジニ不純度, 分類誤差の3種類。prune() で max_depth 以上の枝を事後剪定する。

# -*- coding: utf-8 -*-

import sys
import os
sys.path.append(os.path.join('./decision-tree/'))

import decision_tree as dt
from sklearn.datasets import load_iris


def main():
    d = load_iris()

    tree = dt.DecisionTreeClassifier(
                criterion='entropy',
                pre_pruning=False,
                pruning_method='depth',
                max_depth=3
           )
    tree.fit(d.data[0:150], d.target[0:150])
    tree.show_tree()

    pred = tree.predict(d.data[100:101])
    print(pred, d.target[100:101])


if __name__ == '__main__':
    main()

show_tree() で if/then/else ルールを出力する。scikit-learn と同じルールの決定木となった。

$ python classifier-example.py
 if X[2] <= 2.45
    then {value: 0, samples: 50}
    else if X[3] <= 1.75
        then if X[2] <= 4.95
            then {value: 1, samples: 48}
            else {value: 2, samples: 6}
        else if X[2] <= 4.85
            then {value: 2, samples: 3}
            else {value: 2, samples: 43}

Goの勉強のために移植してみたい。

[1] Information Gain
[2] 1.10. Decision Trees
[3] 決定木アルゴリズム

タグ: Machine Learning

【Python】決定木分類器を書いてみる

決定木