今回は『異常検知と変化検知』 (機械学習プロフェッショナルシリーズ) – 4章 近傍法による異常検知 の 4.1.2 ラベルつきデータに対するk近傍法による異常検知を R で実装してみました。
k近傍法による異常検知
k近傍法 (k-nearest neighbor algorithm) は, 特徴空間上で最も近い距離にある訓練データ (経験分布) に基づいて分類/回帰を行う手法。
参考書では, ラベルがないデータとあるデータの双方に対するk近傍法による異常検知について紹介されている。
ラベルつきデータに対するk近傍法による異常検知は, 異常ラベルのついた近傍標本の数を N^1(x’), 正常ラベルのついた近傍標本の数を N^0(x’) としてベイズの定理から異常度を以下のように定義できる。(参考書から引用)
(1)
D は訓練データ, π^1 は全標本に対する異常標本の割合, π^0 は全標本に対する正常標本の割合とする。
この異常度を用いて異常判定を行うには, 近傍数 k と異常判定の閾値 a_th の2つのパラメータの組を決める必要がある。
パラメータの組を決めるアルゴリズムの大まかな流れは以下。
- D の中から標本 x_n を選ぶ (n = 1,…,N)
- 残りの N – 1 個の標本の中から x_n に最も近い標本を k 個選ぶ
- 式 (1) に基づいて a(x_n) > a_th なら x_n を異常と判定
- N個の標本すべてに判定結果が出揃ったら, F値を求め (k, a_th) の評価値とする
新たな観測値に対しては最大のF値を与えるパラメータを使い異常判定を行う。
R で実装してみた
ラベルつきデータに対するk近傍法による異常検知を R で実装してみる。
今回はコーシー分布から生成した4次元の人工データセットを使う。(異常値の割合は 2%)
library(dplyr)
library(ggplot2)
library(FNN)
set.seed(12345)
n <- 1000
df <- data.frame(
X1 = rcauchy(n, location = 0, scale = 1),
X2 = rcauchy(n, location = 0, scale = 1),
X3 = rcauchy(n, location = 0, scale = 1),
X4 = rcauchy(n, location = 0, scale = 1)
)
df <- df %>%
mutate(y = if_else((X1 * X2 > 80) | (X3 * X4 > 80), T, F))
train_X <-df[1:700,-5]
train_y <- df$y[1:700]
test_X <- df[701:n,-5]
test_y <- df$y[701:n]
table(df$y)
# FALSE TRUE
# 980 20
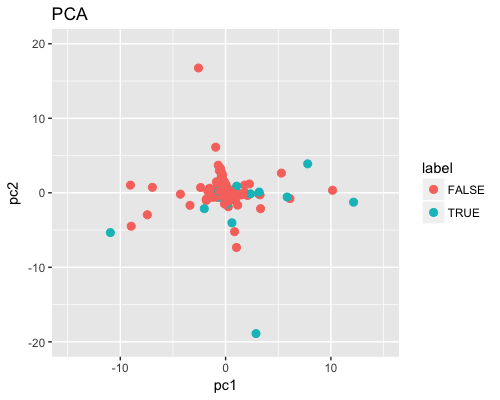
PCA の PC1 と PC2 をプロットすると以下となった。青点が異常値, 赤点が正常値。
pc <- prcomp(df[,-5], scale = TRUE)
df_pc <- data.frame(pc1 = pc$x[,1], pc2 = pc$x[,2], label = df[,5])
g <- ggplot(df_pc, aes(x = pc1, y = pc2)) +
geom_point(aes(colour = label), alpha = 1, size = 2.5) +
labs(title = "PCA", x = "pc1", y = "pc2") +
lims(x = c(-15, 15), y = c(-20, 20))
plot(g)
学習部分は以下で kNN (leave-one-out CV) の計算は {FNN} の knn.cv() を使っている。標本の近さを計る距離はユークリッド距離。
# calculate anomaly score
calc_anomaly <- function(y, idx) {
true <- sum(y)
false <- sum(!y)
eps <- 0.0001
scores <- NULL
for (i in 1:nrow(idx)) {
nn <- c()
for (j in 1:ncol(idx)) {
nn <- c(nn, y[idx[i,j]])
}
t_cnt <- sum(nn)
f_cnt <- ncol(idx) - t_cnt
score <- log((false * t_cnt + eps)/ (true * f_cnt + eps))
scores <- c(scores, score)
}
scores
}
# calculate F-value
calc_f1 <- function(pred, y) {
rec <- sum(y & pred) / sum(y)
prec <- sum(y & pred) / sum(pred)
2 * prec * rec / (prec + rec)
}
ks <- seq(1, 11, 2)
thresholds <- seq(-3, 3, 0.2)
params <- NULL
for (k in ks) {
for (th in thresholds) {
# leave-one-out cross validation
res_cv <- knn.cv(train_X, cl = as.factor(train_y), k = k,
prob = TRUE, algorithm = "kd_tree")
# index of k nearest neighbors
nn_idx <- attr(res_cv, "nn.index")
# calculate anomaly score
scores <- calc_anomaly(train_y, nn_idx)
pred <- if_else(scores > th, T, F)
f_val <- calc_f1(train_y, pred)
params <- rbind(params, c(f_val, k, th))
}
}
新たな観測値に対しては最大のF値を与えるパラメータを使い異常判定を行う。
colnames(params) <- c("f_val", "k", "th")
best_param <- tibble::as_tibble(params) %>%
filter(f_val == max(f_val, na.rm = T))
best_k <- first(best_param["k"][[1]])
best_th <- first(best_param["th"][[1]])
# kNN using best parameter
res <- knn.cv(train = df[,-5],
cl = as.factor(df[,5]),
k = best_k,
prob = TRUE,
algorithm = "kd_tree")
テストデータに対する Accuracy, F-measure は以下となった。
# index of k nearest neighbors
nn_idx <- attr(res, "nn.index")
scores <- calc_anomaly(df[,5], nn_idx)
pred <- if_else(scores > best_th, T, F)[701:n]
table(pred)
# pred
# FALSE TRUE
# 294 6
table(test_y)
# test_y
# FALSE TRUE
# 294 6
# accuracy
sum(pred == test_y)/length(test_y)
# [1] 0.98
df_eval <- df[701:n,] %>%
mutate(label = y,
pred = pred,
pc1 = df_pc$pc1[701:n],
pc2 = df_pc$pc2[701:n]) %>%
mutate(eval = if_else((y == T & pred == T) == T, "TP",
if_else((y == F & pred == F) == T, "TN",
if_else((y == T & pred == F) == T, "FP",
if_else((y == F & pred == T) == T, "FN", "")))))
df_eval$eval <- as.factor(df_eval$eval)
df_eval %>%
group_by(eval) %>%
summarise(n = n())
# # A tibble: 4 x 2
# eval n
#
# 1 FN 3
# 2 FP 3
# 3 TN 291
# 4 TP 3
calc_f1(pred, test_y)
# [1] 0.5
FP (異常の誤検知), FN (異常の見逃し) の確認。
Code は GitHub に置いた。
[1] 【k-NN】R で K 近傍法【はじパタ】
[2] Pythonによる時系列データの異常検知
[3] github.com/twitter/AnomalyDetection
[4] SMOTE で不均衡データの分類