【dlm / Kalman Filter】R による状態空間モデリング

{dlm} を用いた状態空間モデリングの個人的な備忘録です。

はじめに

以下の3つの基本的な状態空間モデルを扱う。環境は macOS 10.12, R 3.3.1, dlm 1.1-4

ローカルレベルモデル
ローカル線型トレンドモデル
季節要素のあるローカル線型トレンドモデル

以下の架空の日次PVデータを用いる。(n=365)

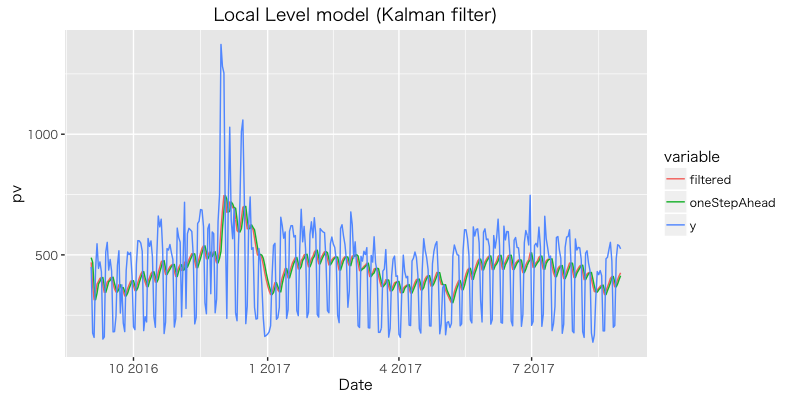
ローカルレベルモデル (ランダムウォークプラスノイズモデル)

ローカルレベルモデルは以下の観測方程式 (上) と状態方程式 (下) からなる。ut はレベル, εt はノイズ (=不規則要素), ξt はレベル撹乱項。

$\begin{eqnarray*} y_t = \mu_t + \epsilon_t, \ \epsilon_t \sim N(0,\sigma^2_\epsilon) \\ \mu_{t+1} = \mu_t + \xi_t, \ \xi_t \sim N(0,\sigma^2_\xi) \end{eqnarray*}$

dlmModPoly() の order に 1 を指定する。 dV, dW はそれぞれ観測ノイズ, システムノイズを指定する。また exp は最尤推定時に分散が負の値になりエラーとなることを回避するため。一期先予測はカルマンフィルタの副産物として得られ dlmFilter() の結果の f に保持される。

buildFunc <- function(parm) {
  dlmModPoly(
    order = 1, # Local Level model (Random Walk plus noise model)
    dV = exp(parm[1]), # variance of the observation noise
    dW = exp(parm[2]) # diagonal elements of the variance matrix of the system noise
  )
}

dlm.mle <- dlmMLE(
  y = df$pv,
  parm = c(0.0001, 0.0001), # vector of initial values
  build = buildFunc,
  method = "L-BFGS-B"
)

dlm.mle$convergence
# [1] 0

dlm.mle$par
# [1] 10.317543  6.021586

dlm.model <- buildFunc(dlm.mle$par)

dlm.filtered <- dlmFilter(df$pv, dlm.model) # Kalman filter

dlm.smoothed <- dlmSmooth(dlm.filtered) # Smoothing

観測値, フィルタ化推定値, 一期先予測を図示。

ローカル線型トレンドモデル

ローカル線型トレンドモデルはローカルレベルモデルに傾き vt (=ドリフト) を導入する。 vt は回帰モデル y = Xβ + ε の傾き β と同じと考える。
状態方程式が1つ増える。

$\begin{eqnarray*} y_t = \mu_t + \epsilon_t, \ \epsilon_t \sim N(0,\sigma^2_\epsilon) \\ \mu_{t+1} = \mu_t + v_t + \xi_t, \ \xi_t \sim N(0,\sigma^2_\xi) \\ v_{t+1} = v_t + \zeta_t, \ \zeta_t \sim N(0,\sigma^2_\zeta) \end{eqnarray*}$

dlmModPoly() の order に 2 を指定する。

buildFunc <- function(parm) {
  dlmModPoly(
    order = 2, # Local Linear Trend model
    dV = exp(parm[1]), # variance of the observation noise
    dW = c(exp(parm[2]), 0) # diagonal elements of the variance matrix of the system noise
  )
}

parm <- log(c(var(df$pv), 0.0001))

dlm.model <- buildFunc(parm)

dlm.filtered <- dlmFilter(df$pv, dlm.model) # Kalman filter

dlm.smoothed <- dlmSmooth(dlm.filtered) # Smoothing

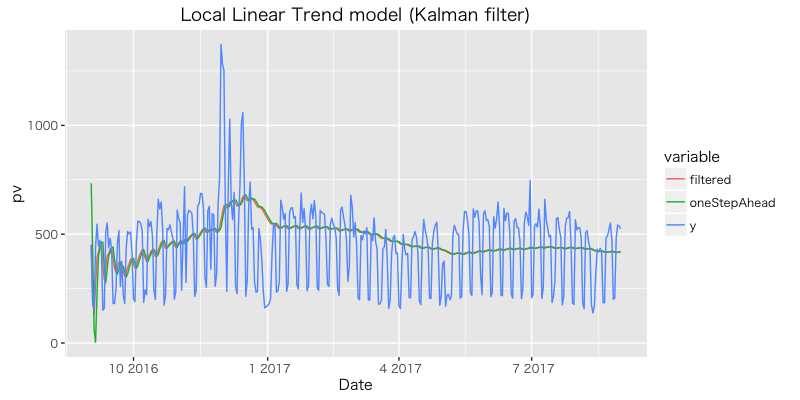
観測値, フィルタ化推定値, 一期先予測を図示。

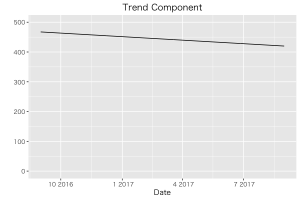
線型トレンドはやや下がり気味。

季節要素のあるローカル線型トレンドモデル

周期性をもつ季節効果を加えたモデル。ローカル線型トレンドモデルに季節要素 γt を加える。

$\begin{eqnarray*} y_t = \mu_t + \gamma_t + \epsilon_t, \ \epsilon_t \sim N(0,\sigma^2_\epsilon) \\ \mu_{t+1} = \mu_t + v_t + \xi_t, \ \xi_t \sim N(0,\sigma^2_\xi) \\ v_{t+1} = v_t + \zeta_t, \ \zeta_t \sim N(0,\sigma^2_\zeta) \\ \gamma_{1,t+1} = -\gamma_{1,t} -\gamma_{2,t} -\gamma_{3,t} \cdots - \gamma_{s-1,t} + \omega_t, \ \omega_t \sim N(0,\sigma^2_\omega) \end{eqnarray*}$

dlmModPoly() に dlmModSeas() を追加する。扱っているのは日次データなので s = 7 として s – 1 = 6つの状態方程式となる。これとは別にフーリエ形式の季節性を表現したい場合は dlmModTrig() が使える。

buildFunc <- function(parm) {
  dlmModPoly(
    order = 2, # Local Linear Trend model
    dV = exp(parm[1]), # variance of the observation noise
    dW = c(exp(parm[2]), 0)) + # diagonal elements of the variance matrix of the system noise
  dlmModSeas(frequency = 7) # seasonal component
}

parm <- log(c(var(df$pv), 0.0001))

dlm.model <- buildFunc(parm)

dlm.filtered <- dlmFilter(df$pv, dlm.model) # Kalman filter

dlm.smoothed <- dlmSmooth(dlm.filtered) # Smoothing

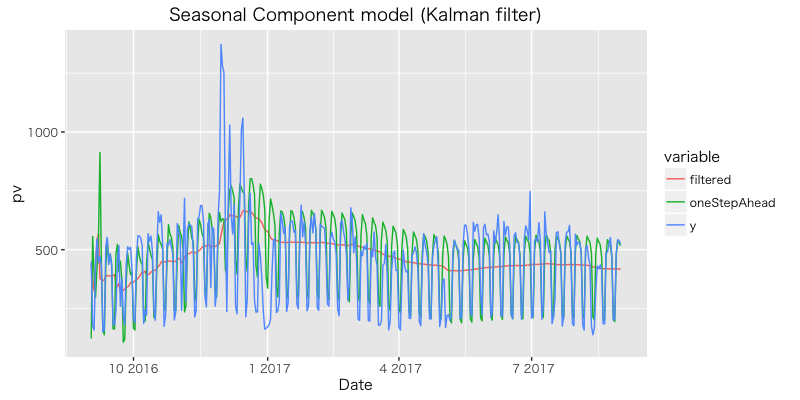
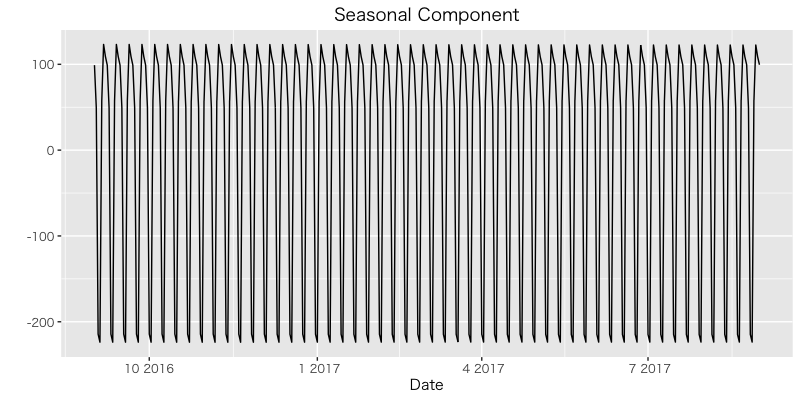
観測値, フィルタ化推定値, 一期先予測を図示。

季節要素の導入により, 平日半ばの pv数が多く土日の pv数が少なくなっているのが表現できている。

> head(dlm.smoothed$s[,3], 7)
[1]  109.07764   99.02605   49.43756 -214.34357 -223.78927   57.43757
[7]  123.15402

状態空間モデルを非線形・非ガウスへ拡張する場合, 今回のカルマンフィルタによるフィルタリングが適用できないため MCMC や逐次モンテカルロ法 (粒子フィルタ) を用いることになる。

データとコードは GitHub に置いた。

おわりに

参考書は以下の3冊で, 理論的な詳細は『状態空間時系列分析入門』の 1-4章, 『カルマンフィルタ ―Rを使った時系列予測と状態空間モデル―』の 2章, 『Rによるベイジアン動的線形モデル』の 2-3章をご覧下さい。

[1] R で状態空間モデル: {dlm} の対数尤度計算について
[2] R で状態空間モデル: {dlm} で単変量モデルの状態空間表現を利用する
[3] Linear State Space Linear Models, and Kalman Filters
[4] How to do model selection in dynamic linear model?