差分の差分法 (Difference-in-differences, DID, DD) を R で試してみます。
- パネルデータ
- 差分の差分法
- 並行トレンド
- Rで差分の差分法
[quads id=1]
パネルデータ
データセットの性質を時間や空間の軸で捉えた場合, 以下に分類できる。
- 時系列データ (Time series data): 1つの項目について時間の経過と共に集めたデータ (時間)
- クロスセクションデータ(Cross section data): ある時点において各地点, グループなど複数の項目を集めたデータ, 横断面データ。 (空間)
- パネルデータ (Panel data): 時系列的性質を持ったクロスセクションデータ。 (時間 x 空間)
DIDではパネルデータを前提としている。計量経済学ではパネルデータと呼ばれるが, 臨床や公衆衛生などの分野では同じような概念を 経時データ [1] と呼んでいるようだ。
差分の差分法
差分の差分法 (Difference-in-differences, DID, DD) では, 処置群 T と対照群 C について処置の前後の2つのタイミングを観測したパネルデータを想定する。
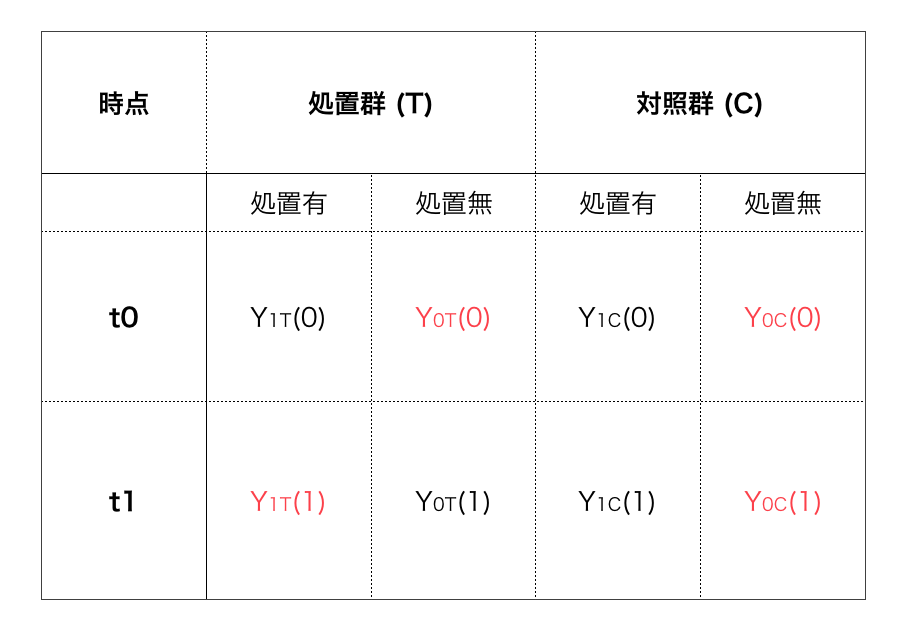
以下の表中の赤字部分の値が観測できたとする。
因果効果と言えるのは, 処置群における Y1T(1) – Y0T(1) または対照群における Y1C(1) – Y0C(1) である。しかし, 当然ではあるが同一個体に対して同時に処置有と処置無を観測することはできない。これは反事実 (counterfactual) と呼ばれる。
このような場合でも反事実を近似して, 平均処置効果 (average treatment effect, ATE) あるいは 処理群の平均処置効果 (average treatment on treated, ATT) を推定する。
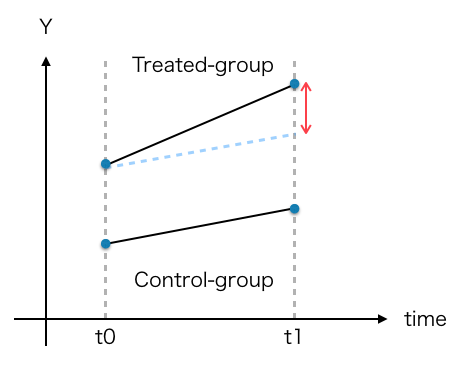
この近似した効果が (Y1T(1) – Y0T(0)) – (Y0C(1) – Y0C(0)) で, 以下の赤矢印の部分にあたる。
赤矢印の部分は, 処置の有無と時点しか説明変数に使ってない下記の単純な線形回帰と一致する。線形回帰なので最小二乗法で推定できるので R や Python 以外のプログラミング言語でも実装し易い。
Y = μ + γ・Tr + δ・t + α(Tr・t) + ε
Trは処置の有無を表すダミー変数, tは時点を表すダミー変数。
並行トレンド
DIDでは, 並行トレンド (parallel trend) の仮定を満たしている必要がある。これは2群が t0 より以前において並行したトレンドを保っていることである。従って, 過去に遡って並行トレンドがあるかどうかを確認する必要がある。これを満たしていることで, 処置群と対照群の割り当てが観察不可能な共変量に基づいている場合でも, 反事実に近づけることができる。
また, 並行トレンドの仮定は短期的には妥当であるが長期になるほど妥当でなくなる点に気をつける必要がある。
実際のDID推定値が妥当なものにするため傾向スコアを用いたマッチングにより対照群を選ぶのがよく使われるようだ。
この時, 傾向スコアは処置への割り当てを目的変数としてロジスティック回帰で求める。この予測結果は処置を受ける確率として解釈できる。
DIDをより一般化した手法として固定効果法 (Fixed Effects, FE) [2] がある。
Rで差分の差分法
RでDIDを試すにあたって, 今回はプリンストン大学の講義資料 [3] に沿って進めてみる。
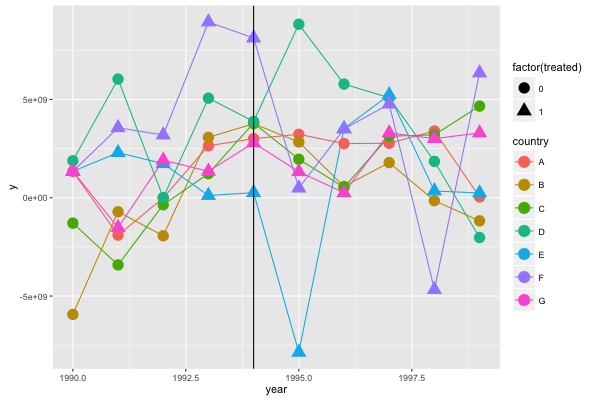
データセット Panel101 は下記から取得する。これが講義のために作られた架空のデータなのか現実世界のデータなのかはわからないが, A-Gまでの7ヶ国についてy, y_bin, x1, x2, x3, opinion を1990年から10年間に渡り記録したパネルデータのようだ。
require(foreign)
# Panel data
panel = read.dta("https://dss.princeton.edu/training/Panel101.dta")
head(panel)
# country year y y_bin x1 x2 x3 opinion
# 1 A 1990 1342787840 1 0.2779036 -1.1079559 0.28255358 Str agree
# 2 A 1991 -1899660544 0 0.3206847 -0.9487200 0.49253848 Disag
# 3 A 1992 -11234363 0 0.3634657 -0.7894840 0.70252335 Disag
# 4 A 1993 2645775360 1 0.2461440 -0.8855330 -0.09439092 Disag
# 5 A 1994 3008334848 1 0.4246230 -0.7297683 0.94613063 Disag
# 6 A 1995 3229574144 1 0.4772141 -0.7232460 1.02968037 Str agree
1994年にE, F, G国で何らかの政策が実施されたとして, この3ヶ国を処置群, それ以外を対照群として前後の y の変化をみるため, ダミー変数を追加する。
# after 1994
panel$postperiod = ifelse(panel$year >= 1994, 1, 0)
panel$treated = ifelse(panel$country == "E" | panel$country == "F" | panel$country == "G", 1, 0)
panel$did = panel$postperiod * panel$treated
DIDで平均処置効果を推定する。
# difference in differences
model.did = lm(y ~ treated + postperiod + did, data = panel)
# p-value 0.0882 : The effect is significant at 10% with the treatment having a negative effect.
summary(model.did)
# Call:
# lm(formula = y ~ treated + time + did, data = panel)
#
# Residuals:
# Min 1Q Median 3Q Max
# -9.768e+09 -1.623e+09 1.167e+08 1.393e+09 6.807e+09
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 3.581e+08 7.382e+08 0.485 0.6292
# treated 1.776e+09 1.128e+09 1.575 0.1200
# time 2.289e+09 9.530e+08 2.402 0.0191 *
# did -2.520e+09 1.456e+09 -1.731 0.0882 .
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 2.953e+09 on 66 degrees of freedom
# Multiple R-squared: 0.08273, Adjusted R-squared: 0.04104
# F-statistic: 1.984 on 3 and 66 DF, p-value: 0.1249
偏回帰係数は -2.520e+09 で, そのp値は 0.0882 となった。自己相関がある場合はどの程度, 気をつけた方が良いのだろうか。
おわりに
今回参考にさせて頂いた本は下記です。
[1] 経時データ: 複数の対象者に対しある反応変数を時間の経過とともに繰り返し測定したデータ
[2] 固定効果モデルの推定
[3] Differences‐in‐Differences (using R)