Rで順序選択モデル (ordered choice model) , 具体的には MASS::polr() で順序ロジットモデル (ordered logit model) と順序プロビットモデル (ordered probit model)を試してみたメモ。
目的変数が質的変数で3択以上の場合の分析
目的変数が質的変数 [1] の場合, {いいえ, はい} のような2択であればダミー変数として0/1に2値化することで, 結果を自然に確率として解釈しても良さそうである。しかし, 3択以上の場合は少し複雑になる。
目的変数が順序尺度の場合
目的変数が {一等, 二等, 三等, その他} のように順序はあるが等距離を仮定できない場合, 質的変数を量的変数に変換して, 一等=3, 二等=2, 三等=1, その他=0 としてモデリングするのは好ましくない。
この場合, 質的変数のままで確率分布にデータにフィットさせる方法があり, 確率分布として正規分布を使う順序プロビットモデル (ordered probit model) と, ロジスティック分布を使う順序ロジットモデル (ordered logit model) が代表的のようだ。
順序ロジットモデルは, 比例オッズモデル (proportional odds model) とも言い, 確率比であるオッズ比 (odds ratio) [2]で説明変数の効果を評価する。
パラメータは尤度関数を最大化する最尤推定量 (MLE) で推定する。
目的変数が順序尺度でない場合
順序をつけられない場合, 離散選択モデル (discrete choice model) である多項ロジットモデル, 多項プロビットモデルを使う方法がある。これらは3つ以上の変数のいずれかを基準点 0 のようなベースカテゴリとして分析する。多項ロジットモデルは IIA (Independence from Irrelevant Alternatives)を仮定する。
順序ロジットモデル / 順序プロビットモデル
今回は目的変数が3択以上の順序尺度の場合を考え, 順序プロビットモデルと順序ロジットモデルを試してみる。
これらのモデルは, 選択結果に対して共通となるようにパラメータ β を制約した上で 選択肢の数 i とした場合の i−1 本の閾値を求める。(閾値メカニズム, threshold mechanism)
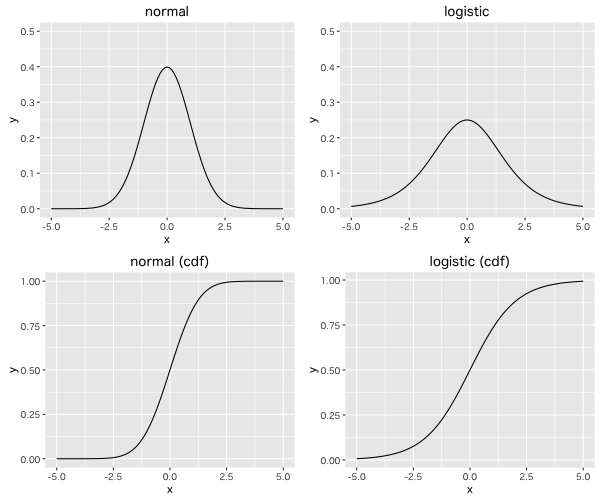
標準正規分布とロジスティック分布の, 確率密度関数 f(x) とその 累積密度関数 F(x) の関係 f(x) = d F(x)/dx は下記のようになる。
累積密度関数は, F(−Inf) = 0, F(Inf) = 1 となる。
理論的にはプロビットモデルが好まれることが多いようだ。一方, プロビットモデルよりロジットモデルの方が傾きの変化の計算が簡単であり, また対数オッズとして解釈がしやすい。
順序ロジットモデル / 順序プロビットモデルの例
順序選択モデルの例として, housingデータセットを取り上げてみる。
順序尺度の因子である家主の満足度とそれに関する3つの因子を持つ。
- Sat: 家主の満足度 (High, Medium or Low, ordered factor).
- Infl: 家主の物件管理における影響力の認知度 (High, Medium, Low).
- Type: 賃貸物件のタイプ, (Tower, Atrium, Apartment, Terrace).
- Cont: 他の住民との関わり度合い (Low, High).
- Freq: 各クラスの住民数.
> head(housing)
Sat Infl Type Cont Freq
1 Low Low Tower Low 21
2 Medium Low Tower Low 21
3 High Low Tower Low 28
4 Low Medium Tower Low 34
5 Medium Medium Tower Low 22
6 High Medium Tower Low 36
housing$Sat が ordered factors型 であることを確認する。[3]
> class(housing$Sat)
[1] "ordered" "factor"
MASS::polr()で順序ロジットモデルを構築する。
> house.plr <- polr(Sat ~ Infl + Type + Cont, weights = Freq, data = housing)
結果から Infl が Medium, High, Contが High の場合に満足度が高くなる傾向がわかる。また, Intercepts の Low|Medium は満足度が Low 以下か, Medium以上かを予測する定数項の推定値である。
目的変数 Sat は High, Medium or Low の3つを取るので, 閾値の推定値は2つ求まる。この閾値間の距離によって, 選択肢間の親近性などがわかる。
> summary(house.plr, digits = 3)
Re-fitting to get Hessian
Call:
polr(formula = Sat ~ Infl + Type + Cont, data = housing, weights = Freq)
Coefficients:
Value Std. Error t value
InflMedium 0.566 0.1047 5.41
InflHigh 1.289 0.1272 10.14
TypeApartment -0.572 0.1192 -4.80
TypeAtrium -0.366 0.1552 -2.36
TypeTerrace -1.091 0.1515 -7.20
ContHigh 0.360 0.0955 3.77
Intercepts:
Value Std. Error t value
Low|Medium -0.496 0.125 -3.974
Medium|High 0.691 0.125 5.505
Residual Deviance: 3479.149
AIC: 3495.149
summaryでもt値が出力されるが, texreg::screenreg() では大まかなp値も出力される。
> texreg::screenreg(house.logit)
Re-fitting to get Hessian
============================
Model 1
----------------------------
InflMedium 0.57 ***
(0.10)
InflHigh 1.29 ***
(0.13)
TypeApartment -0.57 ***
(0.12)
TypeAtrium -0.37 *
(0.16)
TypeTerrace -1.09 ***
(0.15)
ContHigh 0.36 ***
(0.10)
----------------------------
AIC 3495.15
BIC 3538.57
Log Likelihood -1739.57
Deviance 3479.15
Num. obs. 1681
============================
*** p < 0.001, ** p < 0.01, * p < 0.05
method = "probit" を指定することで, 順序プロビットモデルとなる。パラメータの推定値に多少変化があることが確認できる。
> house.probit <- polr(Sat ~ Infl + Type + Cont, weights = Freq, data = housing, method = "probit")
> summary(house.probit, digits = 3)
Re-fitting to get Hessian
Call:
polr(formula = Sat ~ Infl + Type + Cont, data = housing, weights = Freq,
method = "probit")
Coefficients:
Value Std. Error t value
InflMedium 0.346 0.0641 5.40
InflHigh 0.783 0.0764 10.24
TypeApartment -0.348 0.0723 -4.81
TypeAtrium -0.218 0.0948 -2.30
TypeTerrace -0.664 0.0918 -7.24
ContHigh 0.222 0.0581 3.83
Intercepts:
Value Std. Error t value
Low|Medium -0.300 0.076 -3.937
Medium|High 0.427 0.076 5.585
Residual Deviance: 3479.689
AIC: 3495.689
texreg::screenreg()の結果。
> texreg::screenreg(house.probit)
Re-fitting to get Hessian
============================
Model 1
----------------------------
InflMedium 0.35 ***
(0.06)
InflHigh 0.78 ***
(0.08)
TypeApartment -0.35 ***
(0.07)
TypeAtrium -0.22 *
(0.09)
TypeTerrace -0.66 ***
(0.09)
ContHigh 0.22 ***
(0.06)
----------------------------
AIC 3495.69
BIC 3539.11
Log Likelihood -1739.84
Deviance 3479.69
Num. obs. 1681
============================
*** p < 0.001, ** p < 0.01, * p < 0.05
predict() で予測ができ, type = "class" を指定すると, 因子を返し type = "probs" を指定するとそれぞれの因子の選択確率を返す。
また, confint()はパラメータの信頼区間を出力する。
順序選択モデルについての検定は尤度比検定, Wald Test などがある。[6, 7]
順序選択モデリングは {ordinal} パッケージの clm を使う方法もある。 パラメータ推定の方法が違うかもしれないので MASS::polr で上手く推定できない場合は使ってみる手はあるかもしれない。
Codeは GitHub に置いた。
[1] 名義尺度, 順序尺度を質的変数, 間隔尺度, 比率尺度または比例尺度を量的変数と分類する。
[2] ある事象の確率を p とした時, オッズは Odds = p/(1-p) で 2つのオッズの比をオッズ比, ロジットは対数オッズで logit(p) = log(p/(1-p))
[3] 型変換が必要な場合は, factor(c("三等", "二等", "一等"), levels=c("三等", "二等", "一等"), ordered = TRUE) のようにする。
[4] ロジット分析とプロビット分析
[5] ロジットとプロビットの使い分け
[6] 順序選択モデル
[7] 一般化線形モデルと検定