以前, Rの {forecast}, {quantmod} でトレンドを把握したり, 一期先の株価を大まかに予測しましたが, 今回は金融リスクの指標である VaR を計算してみます。
参考にさせて頂いた書籍は確率・統計でわかる「金融リスク」のからくり (ブルーバックス)
ボラリティリティ
金融リスク分析では, 将来の株価の方向は予想できないという立場に立ち, どのくらい上昇・下落のバラつき, つまり リスク [1]があるかを過去の変動パターンを集め統計的な推定を行う。
ボラティリティ (Volatility) は相場の変化率の標準偏差 σ である。一方で 収益率 (リターン)を μ として, 正規分布 N(μ, σ) に対応させる。実際には fat tail が起きやすく正規分布に当てはまらないこともあるが, ランダムに変動する効率的市場仮説の考えに沿っていることや計算の簡便さもありよく使われる。
ボラティリティはヒストリカルボラティリティ (Historical Volatility, HV; Realized Volatility, RV) と インプライドボラティリティ (Implied Volatility, IV) に分類される。
HVは過去のデータに基づき変化率を計算する。ボラティリティは不安定で経済情勢によってもボラティリティは影響を受けやすい。従って, できるだけ長期の観測期間のデータを使って計算した方が良さそうだが, 当然ながらそれでも過去に起きていない規模のバブルや金融危機はデータに含まれないこととなる。
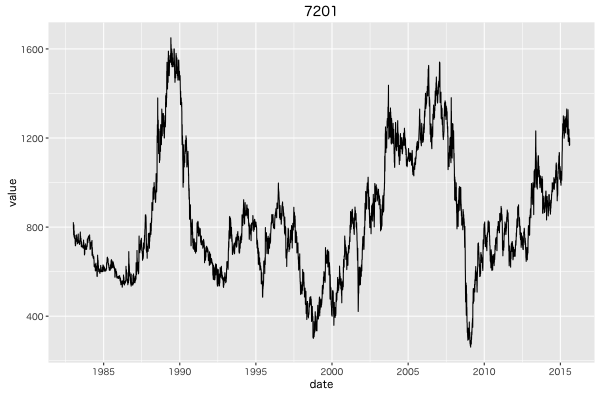
Yahoo Finance で取得した 日産自動車 (7201) の日足(終値)データでHVを計算する。
保有期間を 1日, 5日(1週間), 20日(1ヶ月), 観測期間を 20日(1ヶ月), 250日(1年間), 750日(3年間)とした。
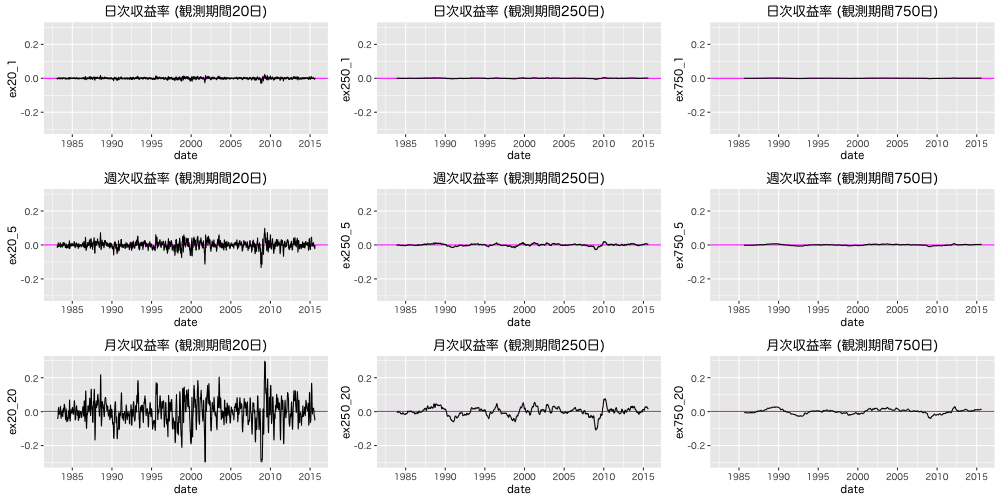
まずは正規分布の平均に相当する対数収益率を計算する。各時間 t で 保有期間の対数収益率を計算してから, zoo::rollapply() で window (観測期間) を移動させながら期間内の平均値を計算する。
観測期間が長期になるほど, 0 に近づく。VaRの計算でリターンはざっくりと 0 としている例もあり, 対象の相場にも依りそうだが妥当そうな感じはある。
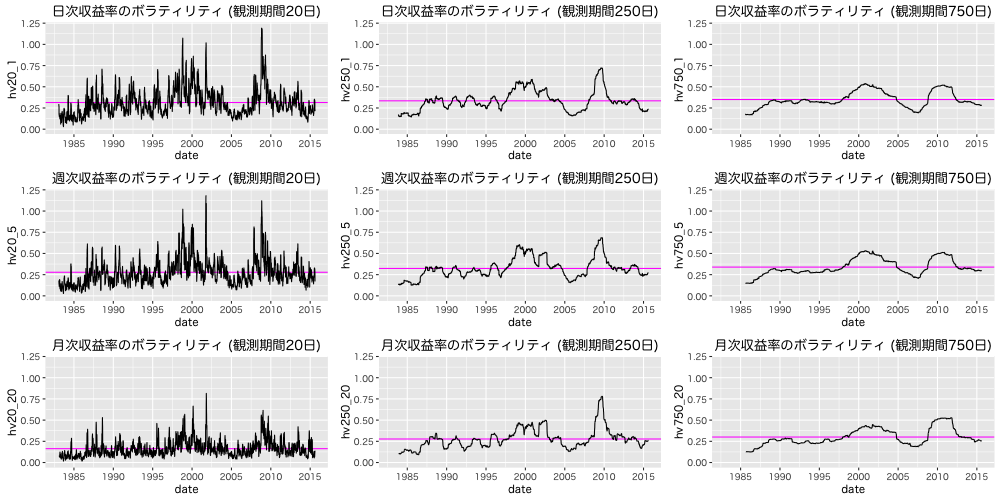
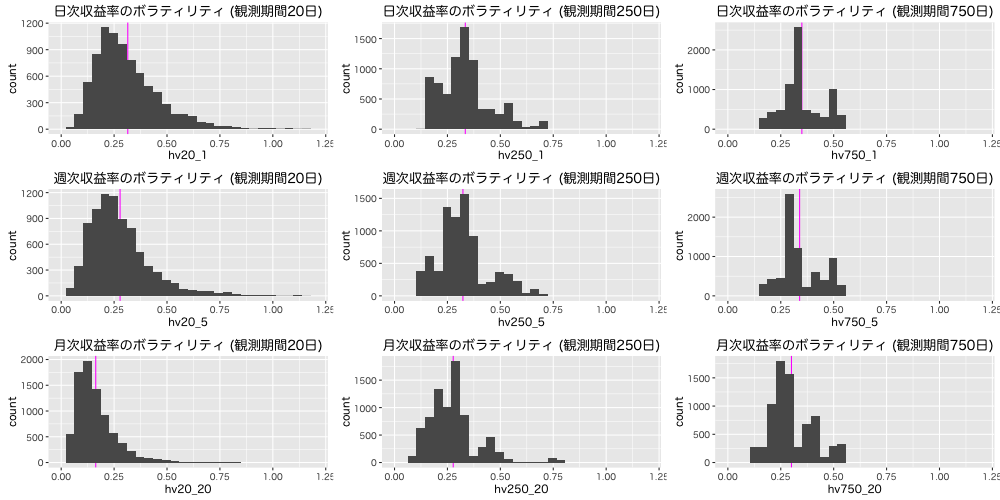
続いて, HV。こちらは √T をかけて年率に換算 (保有期間調整)している。リーマンショック頃にボラティリティが高くなっている。
HVはどの保有期間でも観測期間750日で 平均年率0.30程度となった。この結果だけ見ると, 長期投資はリスクが低いというのは正しくなさそうだ。
VaR
VaR (Value at Risk) は金融リスク分析で広く使われているリスク指標である。投資判断において最大損失金額を推定したい時に役立つ。特に非効率な長期間に渡る塩漬けになるのを防ぐために, 予めリスクを見積もるのは実用的だと思う。
VaRの計算手法には大きく3種類あるようだ。
- 分散共分散法
- ヒストリカル法
- モンテカルロ法
分散共分散法は正規分布を仮定した手法 [3]。ヒストリカル法は過去のデータによる経験分布を用いる手法。また, モンテカルロ法は乱数を用いたシミュレーションによる手法で複雑なモデルも扱える。
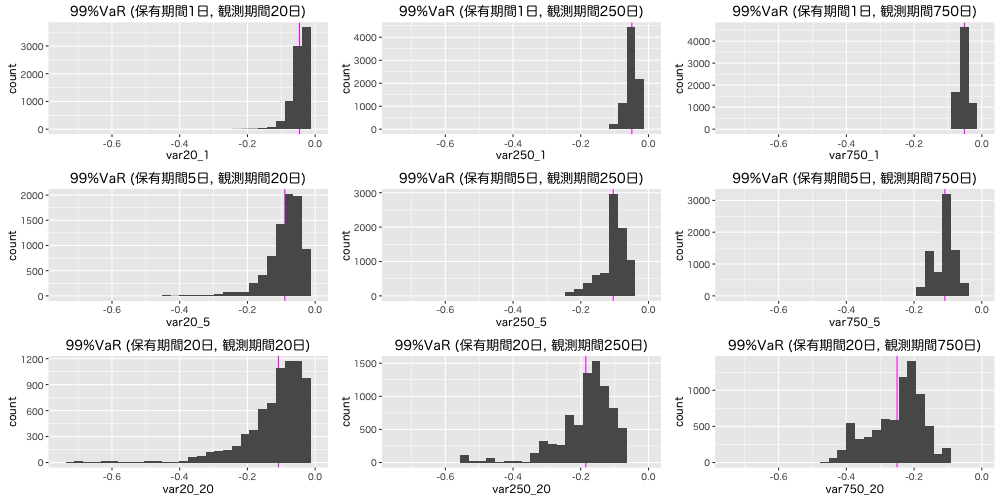
まずは, 分散共分散法で VaR を計算してみる。上記で計算した対数収益率 (リターン) と ボラリティリティを用いて stats::qnorm() で計算する。
信頼水準は99% (σの約2.33倍が99%) とした。これはつまり倒産リスクまでは考えないことに相当する。
上から保有期間が 1日, 5日(1週間), 20日(1ヶ月)のVaR 。保有期間が長い方が VaR が高くなる。
> mean(data$var750_1, na.rm = TRUE)
[1] -0.05139199
> mean(data$var750_5, na.rm = TRUE)
[1] -0.1091336
> mean(data$var750_20, na.rm = TRUE)
[1] -0.2502844
続いて, ヒストリカル法で VaR を計算する。経験分布を使うので実態に近い気がする。一方, より慎重に分析したい場合 99.9…% としたくなるがヒストリカル法では経験分布に依存するため相応のサンプルサイズが必要となりそうだ。
上から保有期間が 1日, 5日(1週間), 20日(1ヶ月)のVaR 。保有期間が長い方が VaR が高くなるのは分散共分散法と同様。
> quantile(data$ex750_1, probs = seq(0.01, 1, 0.33), na.rm = TRUE)[1]
1%
-0.001688636
> quantile(data$ex750_5, probs = seq(0.01, 1, 0.33), na.rm = TRUE)[1]
1%
-0.008419611
> quantile(data$ex750_20, probs = seq(0.01, 1, 0.33), na.rm = TRUE)[1]
1%
-0.03442862
今回のデータでは, ヒストリカル法の方が VaR が低くなった。モンテカルロ法は試していないが VaR は計算する手法によっても結果は大きく変わってくる可能生があるのは注意が必要。
Codeは GitHub に置いた。
長期保有の方が VaR は高くなるが, 長期的には(予測することは困難だとしても)企業の長期的な利益成長を反映するし, 為替相場では購買力平価に沿った動きになる向きもあるので投資目的次第ではある。
次回は {rugarch} を使って, ボラティリティの変動を定式化できる GARCHモデル を試してみる。
[1] リスクはプラスの意味も含まれる。ある意味, 暴落確実な株はリターンがマイナスなだけでリスク自体は低い。
[2] 金融市場の1年間の営業日 250日 または 261日 とすることが多いらしい。
[3] ファットテールの金融商品なら冪乗分布を仮定した方が良さそう。
[4] Ⅰ．市場リスクの計測手法
[5] ヒストリカル法によるバリュー・アット・リスクの計測：市場価格変動の非定常性への実務的対応
[6] xtsパッケージで時系列解析