【異常検知】Deep Learning for Anomaly Detection: A Survey を読んだ (前編)

Deep Learning for Anomaly Detection: A Surveyを読んだので備忘録を残しておきます。異常検知の分野では Anomaly Detection : A Survey [V Chandola, 2009] が有名なサーベイ論文だと思いますが, 深層学習の台頭でアップデートされた部分も多く, 本サーベイ論文は良いガイドラインとなりそうです。References が膨大なため前編/後編に分けます。

導入
異常検知と新規性検知
深層異常検知 (Deep anomaly detection; DAD)
深層学習ベースの異常検知の様々な側面
DAD Models
異常検知における DAD アーキテクチャ
その他の DAD 手法
DAD の相対的な長所と短所
補足: Anomaly Detection using One-Class Neural Networks

導入

深層学習は従来の機械学習と比較して, 以下のようにデータの規模が大きくなるにつれて性能が向上する傾向がある。

本サーベイ論文では深層異常検知 (deep anomaly detection; DAD) の研究について体系的かつ包括的にレビューし, 応用領域への適用や有効性の評価を行っている。

異常検知と新規性検知

異常はデータマイニングや統計学では, 逸脱 (deviants) や外れ値 (outliers) とも呼ばれる（Aggarwal [2013]）

以下の N1, N2 は多くの観測値を含む領域にあり正常なデータインスタンスである。一方, O1, O2, O3 は N1, N2 から離れて位置しており異常とみなせる。

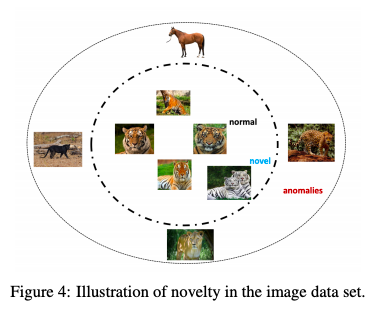
新規性 (novelty) はデータ内の未観察のパターンの識別で, 検出された新規のデータは異常なデータとは見做されない。これまでは見られなかった観測データに対して閾値を用いた novelty score を割り当てる。この閾値から大きく逸脱している場合は異常と見なすことができる。

例えば, トラの画像認識においてホワイトタイガーの画像は新規性と見なされうるが, 他の馬やライオンなどの動物は異常と見なされる。

異常検知で使われるテクニックは新規性検知 (novelty detection) に使用されることがある。

深層異常検知 (Deep anomaly detection; DAD)

従来の外れ値検知アルゴリズムは, 医用画像や系列データの複雑な構造を捉えたり大規模データに対して拡張するのが難しかった。

深層異常検知 (Deep anomaly detection; DAD) は DNN によりデータから複雑で階層的な特徴を学習できる。また, 専門家 (domain experts) による手動の特徴量エンジニアリングが不要となり生データから E2E で学習することができる。

一方, 従来のアルゴリズムと DAD の双方の課題として, 正常データと異常データの境界を正確に定義したり, また異常の継続的な変化に対する対応の難しさがある。

深層学習ベースの異常検知の様々な側面

入力データの性質

異常検知における DNN のアーキテクチャ選択は入力データの性質に依存する。入力データは大きく以下に分類できる。

系列データ: e.g. 音声, テキスト, 音楽, 時系列, タンパク質の配列
非系列データ: e.g. 画像, 挙げられている以外のデータ

系列データに対しては CNN, RNN, LSTM , 非系列データに対しては CNN, AE などのアーキテクチャが選択されることが多い。

入力データは特徴数に応じて低次元データと高次元データに分類される。DAD は高次元の入力データにおける複雑で階層的な特徴の関係性を学習できる。DAD の層の数は入力データの次元により決まり, 深くなるほど高次元データに対して優れた性能が得られる。

ラベルの利用

ラベルはサンプルが正常か異常かを示すが, 異常はレアなため取得することが難しい場合がある。さらに, 異常の振る舞いは時間とともに変化する可能性がある。(Ramotsoela et al. [2018]）

DAD はラベルが利用可能かの視点で3つのカテゴリに分類できる。

教師あり深層異常検知

教師あり深層異常検知 (Supervised deep anomaly detection) は, 正常か異常のラベル付けされたデータインスタンスを用いて二値または多クラス分類器を訓練する。（Chalapathy et al [2016a, b]）
DAD により性能は改善されたが, ラベル付きサンプルが得られないことがあるため半教師ありや教師なし手法ほどには普及していない。さらに, 異常に対して正常なデータインスタンスがはるかに多いクラス不均衡 (class imbalance) のために性能は suboptimal に留まる。

半教師あり深層異常検知

半教師あり深層異常検知 (Semi-supervised deep anomaly detection) は正常なインスタンスが異常に比べて簡単に取得できることから広く使われている。これらの手法は正常なデータから外れ値を分離する。
AE を異常のないサンプルに対して半教師あり手法で訓練すると正常なインスタンスに対して再構成誤差 (reconstruction errors) は低くなることが期待できる。(Wulsin et al. [2010], Nadeem et al. [2016], Song et al. [2017])

教師なし深層異常検知

教師なし深層異常検知 (Unsupervised deep anomaly detection) はデータインスタンスの特徴のみに基づいて外れ値を検知する。ラベル付きデータの取得が難しいため, ラベルなしデータの自動ラベル付けに使用される。(Patterson and Gibson [2017])。従来の PCA, SVM, Isolation Forest より性能が優れている。教師なし深層異常検知モデルの中核は AE である。アルゴリズムは RBM, DBM, DBN, generalized denoising autoencoders, LSTM などがある。

Based on the training objective

目的関数の設計に基づいて DAD は Deep hybrid models (DHM) と One class neural networks (OC-NN) に分類される。

Deep hybrid models (DHM)

DHM では AE を特徴抽出として利用する。AE で学習された特徴は, OC-SVM などの従来の異常検知アルゴリズムに入力される。 Hybrid Models は事前に訓練された転移学習モデルを特徴抽出として用いて成功している（Pan et al, [2010]）

Ergen et al. [2017] では検知性能を最大化するため OC-SVM の目的関数と特徴抽出器を共同訓練する方法を検討した。 Hybrid Models のアプローチの欠点は異常検知のために設計された目的関数が欠けているため, 外れ値を検出するために特化した特徴の抽出に失敗してしまう点である。
Hybrid Models のアプローチの欠点は異常検知のために設計された目的関数が欠けているため, 外れ値を検出するための差分特徴の抽出に失敗してしまう点である。この克服のために, Deep one-class classification (Ruff et al. [2018a]) や One class neural networks (Chalapathy et al. [2018a]) が提案された。

One class neural networks (OC-NN)

One class neural network (OC-NN) (Chalapathy et al. [2018a]) はカーネルベースの one-class classification に影響を受けている。この手法は, 隠れ層のデータ表現が OC-NN の目的関数によって得られるため, AE を特徴抽出として用いて別の異常検知手法 (e.g. OC-SVM) に取り込む Hybrid Models とは異なる。

異常の種類

異常は大きく3つの種類に分類することができる。DAD は全ての種類の異常検知で成功例が示されている。

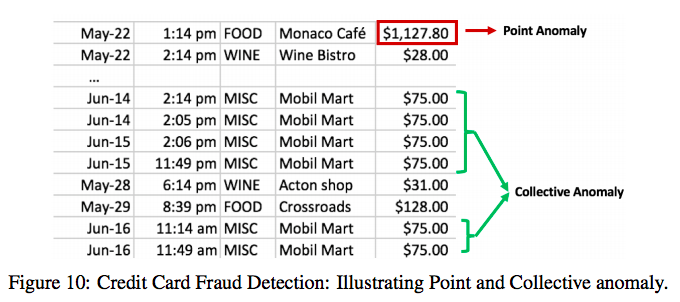
点異常 (point anomalies): 個々のインスタンスが残りのデータに対して異常とみなせる場合. 最も単純なタイプの異常.
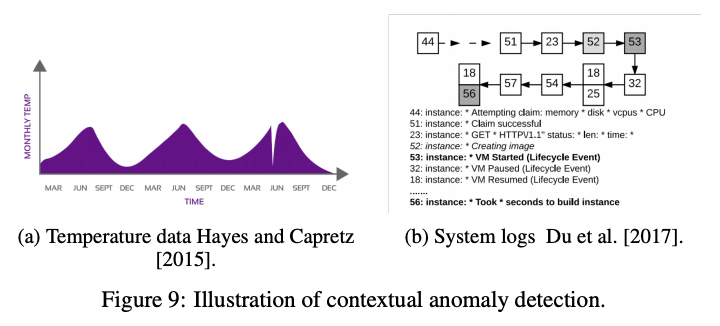
文脈異常 (contextual anomalies): インスタンスが特定の文脈で異常である場合. 文脈的異常は時系列データや空間データに現れる. (e.g. 華氏35度 (摂氏1.6度) は冬では正常だが夏では異常である.)
集合的異常 (collective anomalies): データセットの異常が集合・グループとして関連している場合で, 各インスタンスは個々では異常ではないが集合・グループとして共に現れた場合に異常.

異常スコア

異常スコア (Anomaly score) は各データの異常の度合いを表す。異常スコアはデータインスタンスを順位付けしたり, 異常を判定するために閾値（決定スコア）がその分野の専門家によって選択される。

スコアを割り当てる代わりに, 正常または異常のラベルを各データインスタンスに対して割り当てることがある。

一般に決定スコアは二値ラベルよりも多くの情報を持つ。例えば, Deep SVDD approach では決定スコアは球の中心からの距離である (Ruff et al. [2018b])。

AE を用いた教師なし異常検知は, 再構成誤差に基づき異常スコアを計算し, 専門家によって順位付けまたは閾値が設定される。

DAD Models

以下の DAD モデルについてモデルの仮定, 計算複雑性, 長所と短所の3つの視点で整理する。このフォーマットは Anomaly Detection : A Survey [V Chandola, 2009] に沿っている。

教師あり深層異常検知
半教師あり深層異常検知
ハイブリッド深層異常検知
One-class neural networks (OC-NN)
教師なし深層異常検知

教師あり深層異常検知

教師あり深層異常検知 (Supervised deep anomaly detection) はラベル付きサンプルを使用するため教師なし手法より性能に優れる。 (Gornitz et al. [2013])

仮定: 教師なし手法はデータの特性を説明・理解することにフォーカスするのに対し教師あり手法はクラスの分類に依存している。多クラス異常検知は正常クラスのラベル付きインスタンスが訓練データにあることを前提としている。(Shilton et al. [2013], Jumutc and Suykens [2014], Kim et al. [2015], Erfani et al. [2017])
多クラス異常検知は異常クラスと残りのクラスを区別するように分類器を学習する。ネットワークは特徴抽出とそれに続く分類器に分かれる。特徴表現を学習するためには数千から数百万オーダーの訓練サンプルが必要となるため, 半教師や教師なし手法ほど普及していない。

計算量: 入力データの次元と逆伝播アルゴリズムで訓練された隠れ層の数によって決まる。意味のある階層的な特徴を学習するため高次元データは多くの隠れ層を持つ傾向がある。隠れ層の数とともに線形に増加し, より多くの訓練時間を必要とする。

長所と短所: 教師あり手法は半教師ありや教師なし手法よりも高精度で, 推論段階は高速である。一方, 教師あり手法は正常クラスおよび異常インスタンスに対して正確なラベルが必要となるが利用できない場合が多く, 特徴空間が非線形で非常に複雑な場合に異常データから正常データの分離に失敗する可能性がある。

半教師あり深層異常検知

半教師あり深層異常検知 (Semi-supervised deep anomaly detection) またはone-class DAD では全ての訓練インスタンスに1つのラベルしかないと仮定する。(Kiran et al. [2018] and Min et al. [2018]) 正常インスタンスの周辺の判別境界を学習し, 多数派クラスに属さないテストインスタンスは異常のフラグを立てる。(Perera and Patel [2018], Blanchard et al. [2010])

仮定: 近接性と連続性 (Proximity and Continuity), 入力空間と特徴空間の両方で互いに近い点ほど同じラベルを共有する可能性が高い。DNN の隠れ層内の学習されたロバストな特徴は, 正常なデータと外れ値を区別するための判別性を保持している。

計算量: 計算量は主に入力データの次元と表現を学習する隠れ層の数に依存する.

長所と短所: 半教師あり学習で訓練された GAN はラベル付きデータが非常に少ない場合でも有望である。また, one class のラベル付きデータを使用すると教師なし手法よりも性能が向上する可能性がある。一方, Lu [2009] によって示された半教師あり手法の短所は深層学習の文脈でも当てはまり, 隠れ層内で抽出された階層的な特徴は少数の異常なインスタンスの表現ではない可能性があり, 従って過学習を起こしやすい。

AE: Edmunds and Feinstein [2017] ,Estiri and Murphy [2018]
RBM: Jia et al. [2014]
DBN: Wulsin et al. [2010], Wulsin et al. [2011]
CorGAN, GAN: Gu et al. [2018], Akcay et al. [2018], Sabokrou et al. [2018]
AAE: Dimokranitou [2017]
Hybrid Models (DAE-KNN, DBN-Random Forest, CNN-Relief, CNN-SVM): Song et al. [2017], Shi et al. [2017], Zhu et al. [2018]
CNN: Racah et al. [2017], Perera and Patel [2018]
RNN: Wu and Prasad [2018]
GAN: Kliger and Fleishman [2018], Gu et al. [2018]

ハイブリッド深層異常検知

ハイブリッド深層異常検知はロバストな特徴を学習するための特徴抽出器として広く使用されている。(Andrews et al. [2016a]) 学習された表現は OC-SVM などの従来のアルゴリズムに入力される。Hybrid Models は二段階学習で SOTA を達成することが示されている (Erfani et al. [2016a,b], Wu et al. [2015b])

仮定: DNN の隠れ層で抽出された特徴は, 異常の存在を隠すことができる無関係な特徴を分離することを目的とする。複雑な高次元空間上でロバストな異常検知モデルを構築するには特徴抽出器と異常検知器が必要となる。

計算量: 計算量は DNN と従来のアルゴリズムの両方が含まれる。自明でないDNN アーキテクチャの選択と巨大な空間での最適なパラメータの探索が, Hybrid Models における計算複雑性をもたらす。線形 SVM では入力次元数 d として O(d) となる。多くの多項式や RBF カーネルではサポートベクトルの数 n として O(nd) となるが, RBFカーネル SVM では O(d^2) で近似される。

長所と短所: 特徴抽出器は特に高次元空間での次元の呪いの影響を大幅に減らす。線形モデルまたは非線形カーネルモデルは削減された入力次元で動くため, Hybrid Models はスケーラブルで計算効率が高い。
一方, ハイブリッドアプローチでは異常検知のためのカスタマイズされた目的関数の代わりに一般的な損失関数が使われる。従って, 異常検知器は特徴抽出器の表現学習に影響を与えることができないため suboptimal に留まる。より深い Hybrid Models は個々の層が計算負荷となる場合の方が性能が向上する傾向がある。(Saxe et al. [2011])

AE-OCSVM, AESVM: Andrews et al. [2016a]
DBN-SVDD, AESVDD: Erfani et al. [2016a], Kim et al. [2015]
DNN-SVM: Inoue et al. [2017]
DAE-KNN, DBN-Random Forest, CNN-Relief, CNN-SVM: Song et al. [2017], Shi et al. [2017], Zhu et al. [2018], Urbanowicz et al. [2018]
AE-CNN, AE-DBN: Wang et al. [2018b], Li et al. [2015]
AE+ KNN: Song et al. [2017]
CNN-LSTM-SVM: Wei [2017]
RNN-CSI: Ruchansky et al. [2017]
CAE-OCSVM: Gutoski et al., Dotti et al. [2017]

One-class neural networks (OC-NN)

隠れ層におけるデータ表現は異常検知のためにカスタマイズされた目的関数を最適化することによって学習される。Chalapathy et al. [2018a], Ruff et al. [2018a] では複雑なデータセットにおいて OC-NN が既存の SOTA の手法と同程度の訓練・テスト時間で同等以上の性能を達成できることを実証している。

仮定: OC-NNモデルは DNN の隠れ層内のデータ分布における共通の変動要因を抽出し, テストデータインスタンスに対して外れ値スコアを生成する。異常サンプルに共通の変動要因が含まれないため, 隠れ層は外れ値の表現を捉えることに失敗する。

計算量: DNN の複雑性のみに依存する。 (Saxe et al. [2011]) OC-NN モデルは予測のためにデータを保持する必要がないので省メモリであるが, 訓練時間は入力次元に比例する。

長所と短所: OC-NNモデルは出力空間でデータを囲む超平面 (Chalapathy et al. [2018a]) や超球 (Ruff et al. [2018a]) を最適化しながら DNN と共に訓練する。OC-NNはモデルのパラメータを学習するため交互最小化アルゴリズムを用いる。OC-NNの目的関数の部分問題は well defined である quantile selection problem を解くことと等価である。
短所として, 高次元データでは訓練時間とモデル更新時間が長くなる。また, 入力空間が変化するとモデル更新に時間がかかってしまう。

教師なし深層異常検知

教師なし DAD における困難に対処するいくつかの DNN が提案され SOTA の性能を生み出せることが示されている。異常検知では一般的に AE が使われる。(Baldi [2012])

仮定: データインスタンスの大部分はデータセットの残りの部分と比較して正常で, 潜在的な特徴空間内における正常な領域は異常な領域と区別することができると仮定する。教師なし DAD は距離や密度などデータセットの特性に基づいてデータインスタンスの外れ値スコアを生成する。DNN の隠れ層はデータセット内でこれらの特性を捉えることを目的とする。(Goldstein and Uchida [2016])

計算量: AE は外れ値検知で使われる一般的なアーキテクチャで, 他の NN アーキテクチャと同様に最適化問題は非凸となる。モデルの計算量はネットワークパラメータや隠れ層の数に依存する。AE の訓練の計算量は, 行列分解に基づいている PCA のような従来手法よりもはるかに大きくなる。(Meng et al. [2018], Parchami et al. [2017])

長所と短所: 正常なデータを異常なデータポイントから分離するためのデータの特性を学習する。この手法はデータ内の共通点を特定し外れ値の検出を促す。また, 訓練にラベル付きデータを必要としないため異常を見つけるためのコスト効率に優れる。
一方で, 複雑な高次元空間内のデータ内の共通点を学習するのは困難な場合がある。AE における次元削減の程度は, チューニングが必要なハイパーパラメータであることが多い。教師なし手法はノイズに対して敏感であり, 教師ありや半教師あり手法よりも精度が低い場合が多い。

異常検知における DNN アーキテクチャ

Deep Neural Networks (DNN)

中間層の数が多いディープアーキテクチャ (Schmidhuber [2015], Bengio et al [2009]) は, データ内の新しい変動への一般化 (LeCun et al. [2015]), 従来の機械学習アプローチのスケーラビリティの限界, 手動の特徴エンジニアリングの必要性を克服できる。

Deep Belief Networks (DBNs) は, Restricted Boltzmann Machine (RBM) として知られるグラフィカルモデルの DNN である。異常検知に DBN を用いる仮説は RBM が encoder-decoder ネットワークとして使えるという点である。 (Werbos [1990])
DBN は異常サンプルに対して特徴的な変動を捉えることができないため高い再構成誤差が生じる。DBNはスケーリング可能で解釈可能性を向上できることが示されている。(Wulsin et al. [2010])

Spatio Temporal Networks (STN)

これまで空間的関係と時間的関係の両方の特徴を学習する手法が研究されてきた (Zhang et al. [2018f]). Spatio Temporal Networks (STNs) は時空間特徴を抽出するために CNN と LSTM を組み合わせた DNN アーキテクチャである。時間的特徴 (LSTM で時間的に近いデータ間の相関をモデリング) と空間的特徴（局所 CNN で局所空間的相関をモデリング）が外れ値の検出に有効であることが示されている。 (Lee et al. [2018], SZEKER [2014], Nie et al. [2018], Dereszynski and Dietterich [2011])

Sum-Product Networks (SPN)

積和ネットワーク（Sum-Product Networks; SPN）は葉を変数とした DAG で内部ノードとエッジの重みが和と積を構成する。 SPN は多くの層にわたって高速で正確な確率推論を持つ混合モデルの組み合わせと見なされる。(Poon and Domingos [2011], Peharz et al. [2018])

Word2vec Models

Word2vec は単語埋め込みを生成するために使われる DNN の一種。(Mikolov et al. [2013])。文や時系列データなどのデータインスタンス内の系列的な関係性を捉えることができる。単語埋め込み特徴を取得することはいくつかの深層学習のアーキテクチャの性能を改善することが示され, (Rezaeinia et al. [2017], Naili et al. [2017], Altszyler et al. [2016]) 異常検知モデルの性能を向上できることが示されている。(Schnabel et al. [2015], Bertero et al. [2017], Bakarov et al. [2018], Bamler and Mandt [2017])

Generative Models

生成モデルは変動を伴う新しいデータ点を生成するためにデータ分布を学習することを目的としている。一般的な生成的アプローチは VAE（Kingma and Welling [2013]）と GAN (Goodfellow et al. [2014a,b]) の2つである。

Adversarial autoencoders (AAE)（Makhzani et al. [2015]）として知られる GAN の一種は AE の隠れ層内で学習された潜在的符号に任意の事前分布を課すために敵対的訓練を使用することで, 入力分布を効率的に学習できることが示されている。この入力分布を学習する能力を利用した敵対的生成ネットワークに基づく異常検知フレームワーク (GAN-AD）(Li et al. [2018], Deecke et al. [2018], Schlegl et al. [2017], Ravanbakhsh et al. [2017b], Eide [2018]) は, 高次元で複雑なデータセットの異常識別に効果的であることを示している。

一方で, KNN のような従来法は深層生成モデルと比較し少ない数の異常を持つシナリオにおいてより良く機能することが示されている。(Skv ara et al. [2018])

Convolutional Neural Networks

CNN は画像を分析するための一般的な NN の選択である。 (Krizhevsky et al. [2012]) CNN の複雑な構造を持つ高次元データから特徴を抽出する能力は, 画像データと系列データの両方で異常検知における特徴抽出器として用いられる。 (Gorokhov et al. [2017], Kim [2014])
CNN ベースの異常検知手法の評価は活発な研究領域である。(Kwon et al. [2018])

Sequence Models

RNN (Williams [1989]) は時系列データの特徴を捉えることができる。RNN の限界は time step が増えるにつれて充分にコンテキストを捉えることが難しくなる点である。この問題を解決するために前の time step に関する情報を格納するメモリセルを含む LSTM (Hochreiter and Schmidhuber [1997]) が提案された。
GRU (Cho et al. [2014]) は LSTM と似ているが, 別々のメモリセルでなく情報の流れを制御するために統合された1つのゲートを使用する。
異常検知のための LSTM ベースのアルゴリズムは従来法よりも性能が向上することが報告されている (Ergen et al. [2017])

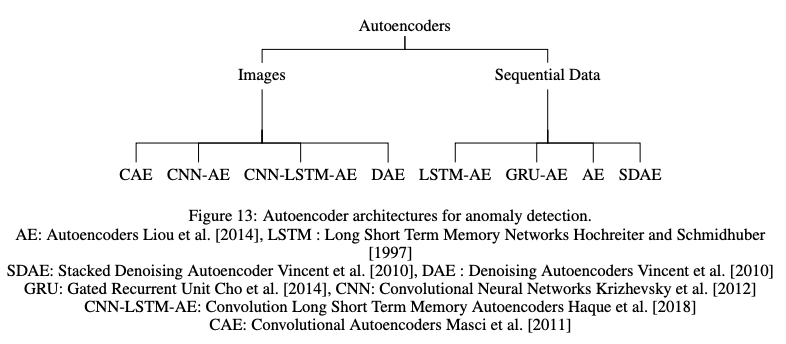
Autoencoders

線形の活性化関数を有する単層の AE は PCA (Pearson [1901]) とほぼ同等である。 PCA は線形の次元削減に制限されるが, AE は線形と非線形の両方の変換を可能にする。 (Liou et al. [2008, 2014])

AE は異常検知に応用されている。AE は複数の隠れ層内で入力データを再構築することによってデータを表現し効果的に識別関数を学習する。正常なデータインスタンスのみで AE を訓練すると, 異常なサンプルに対して再構築に失敗し, 大きな再構成誤差が発生する。従って, 再構成誤差が大きいデータサンプルは異常と見なせる。

AE アーキテクチャの選択はデータの性質に依存する。畳み込みネットワークは画像データに適しており LSTM ベースのモデルは系列データに対して良い結果を生み出す傾向がある。エンコーダを CNN, デコーダを入力画像を再構築する多層の LSTM として組み合わせる試みは, データ内の異常を検知するのに効果的であることが示さている。GRU-AE, CNN-AE, LSTM-AE などの複合的なモデルにより, 人手による特徴量エンジニアリングの必要がなくなり異常検知タスクにおける前処理を容易にする。異常値検知において AE はシンプルで効果的なアーキテクチャであるが, ノイズの多い訓練データの場合に性能が低下する。 (Zhou and Paffenroth [2017])

その他の DAD 手法

転移学習

Litjens et al. [2017] と Pan et al. [2010] は転移学習 (Transfer Learning)をレビューし, 深層学習は良い特徴表現を学ぶために十分なデータが必要であることを説明している。転移学習は不十分な訓練データの根本的問題を解決するために欠かせないツールである。転移学習は訓練データと将来のデータが同じ特徴空間で同じ分布を持つという仮定を緩めることでソース領域からターゲット領域に学習されたモデルを適用させることを目的としている。転移表現学習は (Andrews et al. [2016b], Vercruyssen et al. [2017], Li et al. [2012], Almajai et al. [2012], Kumar and Vaidehi [2017], Liang et al. [2018]) によって研究され有望な結果が示されている。

Zero Shot learning

Zero Shot learning （ZSL）は訓練セット内で見たことのないオブジェクトを認識することを目的としている。(Romera-Paredes and Torr [2015])
ZSL は自然言語の記述や属性におけるオブジェクトに関する知識（メタデータ）を取得し, この知識を使用し新しいクラスセットのインスタンスを分類する。この設定は現実世界の訓練ではすべてのクラスの画像を得ることができない可能性があるため重要である。

異常検知と新規性検知において ZSL を用いたアプローチは SOTA を達成している。 (Mishra et al. [2017], Socher et al. [2013], Xian et al. [2017], Liu et al. [2017], Rivero et al. [2017]) このアプローチの主な課題はデータインスタンスに関するメタデータを取得することである。

アンサンブル法

DNN の課題は入力データのノイズに敏感でありロバストな動作のためには大規模な訓練データが必要となることが多い点である。(Kim et al. [2016]) ノイズの多いデータでもロバスト性を得るため AE の接続アーキテクチャをランダムに変化させるというアイデアによって非常に良い性能が得られることが示された

AE のアンサンブルは複数のベンチマークデータセットで有望な結果を達成した。(Chen et al. [2017]) 多様性を向上するアンサンブルアプローチは訓練時間を短縮しつつ過学習を回避できる。

クラスタリング

クラスタリングに基づく異常検出は Ester et al. [1996] により提案された。クラスタリングは抽出された特徴に基づいて似ているパターンをグループ化して新しい異常を検出する。クラスタリングのクラス数により時間/空間計算量は線形に増加する。 (Sreekanth et al. [2010]) 複雑で高次元のデータセットに対してもスケーラビリティが確保される DNN では, 隠れ層内の特徴抽出により次元数は削減される。DAD のクラスタリングアプローチ, 例えば word2vec モデルではデータの意味表現からクラスタを形成し異常を検出する。 (Yuan et al. [2017])

DAD の相対的な長所と短所

与えられた異常検知問題のコンテキストに対して, どの異常検知手法が最も適しているかを理解することが重要である。しかし, DAD が活発な研究分野であることを踏まえると, あらゆる異常検知問題に対してそのような理解を提供することは難しい。従って, ここでは単純な問題設定について様々なカテゴリの手法の相対的な長所と短所を分析する。

分類ベースの教師あり DAD は, 正常インスタンスと異常インスタンスの均衡が取れているシナリオにおいて良い選択である。教師付き DAD の手法の計算量は現実の問題に適用されるときに重要な側面である。分類ベースの教師あり又は半教師ありの手法は訓練に時間がかかるが, テストは事前に訓練されたモデルを使用するため高速である。

ラベル収集はコストと時間がかかるプロセスのため, 教師なし DAD の手法が広く使われている。教師なし DAD の多くは異常分布を仮定する事前分布が必要なためノイズの多いデータではあまりロバストではない。

Hybrid Models は DNN の隠れ層内のロバストな特徴を抽出し, OC-SVMのような従来の異常検知アルゴリズムにフィードされる。このアプローチは隠れ層での表現学習に影響を与えることができないため性能は suboptimal に留まる。

OC-NN は DNN のデータの豊富な表現を抽出する機能と one-class の目的関数を組み合わせることで正常なデータポイントを異常なデータポイントから分離する機能を兼ね備える。このアーキテクチャの利点をより理解するためにはさらなる研究が必要である。

Anomaly Detection using One-Class Neural Networks

Deep Learning for Anomaly Detection: A Survey で何度か言及されている OC-NN (Chalapathy et al. [2018a]) は異常検知で広く使われている OC-SVM (Scholkopf and Smola [2002]) を NN アーキテクチャに統合するための方法を提案している。
OC-SVM は SVM の特別なケースで, 以下の目的関数により reproducing kernel Hilbert space (RKHS) 上において原点からすべてのデータ点を分離するように超平面 (超球) を学習する。すべてのデータ点は正例のインスタンス (正常) と見なされ, 原点は負例 (異常) と見なされる。w は超平面に垂直なノルム, r は超平面のバイアスである。

$\begin{eqnarray*} min_{\omega, r} \frac{1}{2} \| \omega \|_{2}^{2} + \frac{1}{\nu} \cdot \frac{1}{N} \sum_{n=1}^{N} max(0, r - \langle \omega, \Phi(X_{n\:}) \rangle) - r \end{eqnarray*}$

OC-NN は OC-SVM のような目的関数を使用して NN の訓練を行う。線形またはシグモイドの活性化関数を持つひとつの隠れ層と出力ノードから成るシンプルな feed forward network の場合, OC-NN の目的関数は以下となる。w は隠れ層から出力層へのスカラー値, V は入力から隠れ層への重み行列である。

$\begin{eqnarray*} min_{\omega, V, r} \frac{1}{2} \| \omega \|_{2}^{2} + \frac{1}{2} \| V \|_{F}^{2} + \frac{1}{\nu} \cdot \frac{1}{N} \sum_{n=1}^{N} max(0, r - \langle \omega, g(VX_{n\:}) \rangle) - r \end{eqnarray*}$

OC-SVM との主要な違いは内積部分を置き換えている点である。学習済みの AE に異常検知用としてレイヤーを追加できる一方で, この目的関数は非凸となりパラメータ推論のためのアルゴリズムは大域的最適化には繋がらなくなってしまう。OC-NN ではパラメータ w, r を学習するため, 交互最小化アルゴリズムを用いる。OC-NN の全体のアルゴリズムは以下。

まず, NN のパラメータ w 及び V は通常の BackProp により求める。次に, 異常の割合を制御するパラメータ ν によるスコアの分位数を使って r を求める。 (quantile selection problem)
この手順を収束まで繰り返し, 最終的に得られる決定スコアは S_n = y_hat_n − r で求め, 0 以上の場合は正常, 0 未満の場合は異常と判定する。

[1] データインスタンスは属性 (変数, 特徴, フィールド, 次元) を持つ単変量または多変量で構成される。変数は二値, カテゴリ値, 連続値である。