前回に引き続き, 画像処理の基礎を OpenCV3 を使って勉強します。参考書籍は,『OpenCVによる画像処理入門』です。
実行環境は前回と同様です。macOS Sierra, Python 2.7.12。
In [1]: import cv2
...: import numpy as np
...: from matplotlib import pyplot as plt
今回は以下の画像処理, 主にフィルタ処理を試してみます。
- 平滑化フィルタ
- エッジ検出フィルタ
- 二値画像処理
- 画像間演算
平滑化フィルタ
入力画像の各画素値だけでなく, 周辺領域の画素値も使って出力値を求めるような領域に基づく濃淡変換を 空間フィルタリング という。
中でも オペレータ (カーネル) という矩形の重み付けのための行列を用いて畳み込み演算を行うことを 線形フィルタ という。また, 畳み込み演算を伴わない場合を 非線形フィルタ という。
滑らかな濃淡変化を与える処理を平滑化という。
まずは, 移動平均オペレータによる平滑化フィルタ。
In [2]: img_src = cv2.imread('../images/Lenna.jpg', cv2.IMREAD_COLOR)
In [3]: img_dst = cv2.blur(img_src, ksize=(5,5))
In [4]: cv2.imshow('Normalized box filter', img_dst)
In [5]: cv2.waitKey(0)
Out[5]: 113
加重平均オペレータの中で, 重み付けに正規分布を用いた場合をガウシアンフィルタという。
標準偏差 σ を大きくすると平滑化度合いが増えていく。
In [6]: img_dst = cv2.GaussianBlur(img_src, ksize=(5,5), sigmaX=1)
In [7]: cv2.imshow('Gaussian', img_dst)
In [8]: cv2.waitKey(0)
Out[8]: 113
単純な平均化オペレータでは境界がぼやける欠点があるが, 距離だけでなく注目画素との画素値の差によって重み付けを行う バイラテラルオペレータ ではこれが改善される。ノイズを軽減しつつ画像のエッジを保存する。
In [9]: img_dst = cv2.bilateralFilter(img_src, d=5, sigmaColor=50, sigmaSpace=100)
In [10]: cv2.imshow('Bilateral', img_dst)
In [11]: cv2.waitKey(0)
Out[11]: 113
ノイズの尺度には SN比 [dB] がよく用いられる。σs を信号の実効値, σn をノイズの実効値として SN比は以下となる。
中央値フィルタは畳み込みはせずに注目画素の周辺領域内の全ての画素をソートして, その中央値を注目画素の画素値とする。
中央値を使うことでスパイクノイズの除去に有効。
In [12]: img_dst = cv2.medianBlur(img_src, ksize=5)
In [13]: cv2.imshow('Median', img_dst)
In [14]: cv2.waitKey(0)
Out[14]: 113
エッジ検出フィルタ
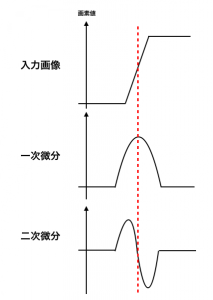
微分オペレータは隣接する画素値の勾配を求める。勾配が大きい部分を抽出することで画像の境界 (Edge) を検出する。[1] 縦方向と横方向の微分オペレータがあり, 横方向の微分は縦方向のエッジを検出, 縦方向の微分は横方向のエッジを検出する。
Sobelオペレータは微分オペレータで生じやすいノイズに反応してしまう問題を解決するため微分方向とは別方向に平滑化を行う。
これにより滑らかにエッジを抽出できる。
In [15]: img_tmp = cv2.Sobel(img_src, ddepth=cv2.CV_32F, dx=1, dy=0)
In [16]: img_dst = cv2.convertScaleAbs(img_tmp)
In [17]: cv2.imshow('Sobel', img_dst)
In [18]: cv2.waitKey(0)
Out[18]: 113
また, 画像の横方向の二次微分と縦方向の二次微分の結果を足してラプラシアン求めた場合を ラプラシアンフィルタ という。注目画素の周りが似ていればラプラシアンは0に近い値となり, ヒストグラムは 0 の辺りに山を作る。方向に依存しないエッジを求められる。
ただし, ノイズを強調してしまうためにガウシアンフィルタを適用し平滑化した後に, ラプラシアンフィルタを用いられることがよくある。 (LoGフィルタ)
鮮鋭化フィルタ (sharpning filter) は隣接する画素の画素値の差分を大きくする処理。つまり元の画像の濃淡を残したままエッジを強調する。
In [19]: k = 1.0
In [20]: op = np.array([[-k, -k, -k], [-k, 1+8*k, -k], [-k, -k, -k]])
In [21]: img_tmp = cv2.filter2D(img_src, ddepth=-1, kernel=op)
In [22]: img_dst = cv2.convertScaleAbs(img_tmp)
In [23]: cv2.imshow('Sharpening', img_dst)
In [24]: cv2.waitKey(0)
Out[24]: 113
二値画像処理
二値化処理では画像を白黒に変換する。閾値を変化させると出力画像で表示される白と黒の割合が変化する。
In [25]: img_gry = cv2.cvtColor(img_src, cv2.COLOR_BGR2GRAY)
In [26]: thresholds = [50, 100, 150, 200, 250]
In [27]: ret, img_dst1 = cv2.threshold(img_gry, thresholds[0], 255, cv2.THRESH_BINARY)
In [28]: ret, img_dst2 = cv2.threshold(img_gry, thresholds[1], 255, cv2.THRESH_BINARY)
In [29]: ret, img_dst3 = cv2.threshold(img_gry, thresholds[2], 255, cv2.THRESH_BINARY)
In [30]: ret, img_dst4 = cv2.threshold(img_gry, thresholds[3], 255, cv2.THRESH_BINARY)
In [31]: ret, img_dst5 = cv2.threshold(img_gry, thresholds[4], 255, cv2.THRESH_BINARY)
In [32]: titles = ['original','threshold=50','threshold=100',
...: 'threshold=150','threshold=200','threshold=250']
In [33]: images = [img_gry, img_dst1, img_dst2, img_dst3, img_dst4, img_dst5]
In [34]: for i in xrange(6):
...: plt.subplot(2,3,i+1),plt.imshow(images[i],'gray')
...: plt.title(titles[i])
...: plt.xticks([]),plt.yticks([])
...:
In [35]: plt.show()
マスク処理は不必要とする部分を完全に消去し必要な領域のみを抽出する処理。
マスク処理はクロマキー合成などで使われる。[2]
In [36]: img_src = cv2.imread('../images/Lenna.jpg', cv2.IMREAD_GRAYSCALE)
In [37]: img_msk = cv2.imread('../images/Mask.jpg', cv2.IMREAD_GRAYSCALE)
In [38]: img_dst = cv2.bitwise_and(img_src, img_src, mask=img_msk)
In [39]: cv2.imshow('Masking', img_dst)
In [40]: cv2.waitKey(0)
Out[40]: 113
モルフォロジー演算 (Morphological Operations) とは膨張・収縮処理によって独立点や突起を除去するような演算。
膨張処理 (dilation) は図形を外側に1画素分広げる処理, 収縮処理 (elosion) は図形を内側に1画素分狭める処理。
膨張・収縮処理では一方のノイズが除去できるが他方のノイズが増大してしまうため, 膨張処理n回後に収縮処理をn回行う クロージング や, 逆に収縮処理n回後に膨張処理をn回行う オープニング が使われる。クロージングでは, 小さな孔を塞ぎ分断された連結要素を接続, オープニングでは小さな孤立点を取り除ける。
In [41]: kernel = np.ones((5,5), np.uint8)
In [42]: img_elosion = cv2.erode(img_gry, kernel, iterations=1)
In [43]: img_dilation = cv2.dilate(img_gry, kernel, iterations=1)
In [44]: img_close = cv2.morphologyEx(img_gry, cv2.MORPH_CLOSE, kernel)
In [45]: img_open = cv2.morphologyEx(img_gry, cv2.MORPH_OPEN, kernel)
In [46]: images = [img_src, img_gry, img_elosion, img_dilation, img_close, img_open]
In [47]: titles = ['original', 'gray', 'elosion', 'dilation', 'closing', 'opening']
In [48]: for i in xrange(6):
...: plt.subplot(2,3,i+1),plt.imshow(images[i],'gray')
...: plt.title(titles[i])
...: plt.xticks([]),plt.yticks([])
...:
In [49]: plt.show()

二値画像内に存在する一連の繋がった要素をブロブ (blob) という。
ラベリング処理は二値画像内に複数のブロブが存在する場合に id をつける処理を指す。
以下では, ブロブを cv2.connectedComponents() で探しそれぞれのブロブに色を振っている。
In [53]: import copy
In [54]: import random
In [55]: img_src = cv2.imread('../images/Label.jpg', cv2.IMREAD_COLOR)
In [56]: img_dst = copy.copy(img_src)
In [57]: img_dst = copy.copy(img_src)
In [58]: img_gry = cv2.cvtColor(img_src, cv2.COLOR_BGR2GRAY)
In [59]: ret, th = cv2.threshold(img_gry, 0, 255, cv2.THRESH_BINARY | cv2.THRESH_OTSU)
In [60]: labels, img_obj = cv2.connectedComponents(th)
In [61]: labels
Out[61]: 4
In [62]: colors = []
In [63]: for i in xrange(1, labels+1):
...: colors.append(np.array([random.randint(0, 255), random.randint(0, 255), random.r
...: andint(0, 255)]))
...:
In [64]: for y in xrange(0, height):
...: for x in xrange(0, width):
...: if img_obj[y, x] > 0:
...: img_dst[y, x] = colors[img_obj[y, x]]
...: else:
...: img_dst[y, x] = [0, 0, 0]
...:
In [65]: output = cv2.connectedComponentsWithStats(th, connectivity=4, ltype=cv2.CV_32S)
In [66]: labels, labels, stats, centroids = output[:4]
In [67]: centroids
Out[67]:
array([[ 193.68297301, 199.74156815],
[ 361.5 , 117.5 ],
[ 202.50426141, 192.49277413],
[ 78. , 332.5 ]])
In [68]: cv2.namedWindow("Source", cv2.WINDOW_AUTOSIZE)
In [69]: cv2.imshow("Source", img_src)
In [70]: cv2.namedWindow("Connected Components", cv2.WINDOW_AUTOSIZE)
In [71]: cv2.imshow("Connected Components", img_dst)
In [72]: cv2.waitKey(0)
Out[72]: 113
画像間演算
複数枚の画像を入力として, それぞれの画像の同じ位置にある画素ごとに決められた演算を行い出力値を決定する処理を 画像間演算 という。
アルファブレンディングは2枚の画像の同位置にある2つの画素値の重み付き平均値を出力する。 α を画像位置で変化させることで様々な効果が得られる。cv2.addWeighted() で求まる。
In [2]: img_src1 = cv2.imread('../images/Lenna.jpg', cv2.IMREAD_GRAYSCALE)
In [3]: img_src2 = cv2.imread('../images/Mask.jpg', cv2.IMREAD_GRAYSCALE)
In [4]: img_dst = cv2.addWeighted(src1=img_src1, alpha=0.5, src2=img_src2, beta=0.5, gamma=0.0)
In [5]: cv2.imshow('Alpha Blending', img_dst)
In [6]: cv2.waitKey(0)
Out[6]: 113
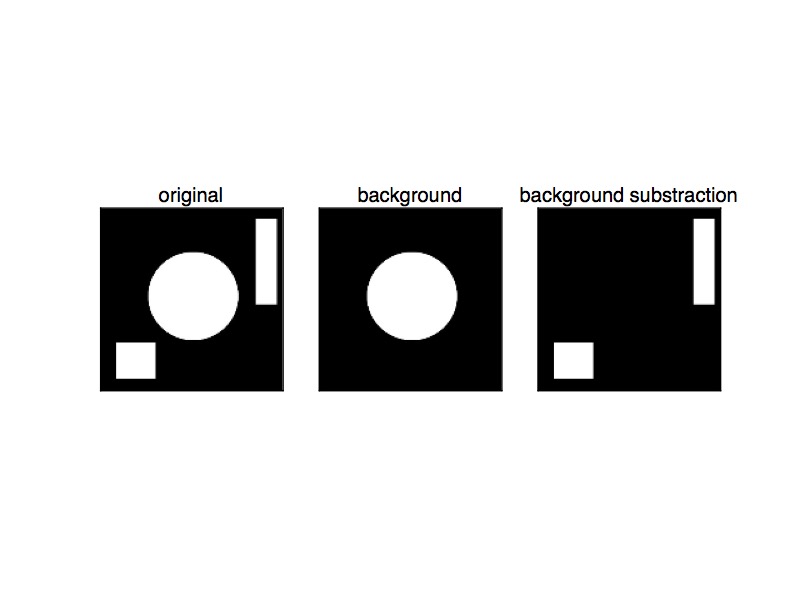
移動物体が入ったような画像から移動物体領域だけを切り出した画像を取得する場合は 背景差分 を求める。
注意点として, 通常は差分画像に対して閾値処理をした画像には小さな孔や連結部分が含まれるため膨張・収縮処理を行い除去する。
In [7]: img_src = cv2.imread('../images/Label.jpg', cv2.IMREAD_GRAYSCALE)
In [8]: img_bkg = cv2.imread('../images/Mask.jpg', cv2.IMREAD_GRAYSCALE)
In [9]: img_diff = cv2.absdiff(img_src, img_bkg)
In [10]: ret, img_bin = cv2.threshold(img_diff, 50, 255, cv2.THRESH_BINARY)
In [11]: kernel = np.ones((3,3), np.uint8)
In [12]: img_dilation = cv2.dilate(img_bin, kernel, iterations=4)
In [13]: img_msk = cv2.erode(img_dilation, kernel, iterations=4)
In [14]: img_dst = cv2.bitwise_and(img_src, img_msk)
In [15]: cv2.imshow('Background Substraction', img_dst)
In [16]: cv2.waitKey(0)
Out[16]: 113
Code は GitHub に置きました。
[1] エッジの定義は, 画像中で明るさが急に変化する部分
[2] クロマキー合成はある色を透過色に設定することで画像の必要な部分のみを抽出し複数の画像を合成する処理で, 天気予報の映像で使われたりする。