【Python】回帰木 (決定木) を書いてみる

前回は分類問題における決定木, 分類木 (classification tree) を書いてみましたが, 今回は前回のコードを拡張して回帰問題における決定木, 回帰木 (regression tree) に対応させてみます。

回帰木は “Python機械学習プログラミング達人データサイエンティストによる理論と実践” の第10章多項式回帰で触れられています。

回帰木

目的関数は分類木の場合と同様で以下。

$\begin{eqnarray*} IG ( D_{p}, f ) = I(D_{p}) - \frac {N_{left}} {N_{p}} I(D_{left}) - \frac {N_{right}} {N_{p}} I(D_{right}) \end{eqnarray*}$

f は特徴量, Dpは親データセット, Dleft, Drightは子ノード。

分割条件を MSE (Mean Squared Error) とした場合, ノード t の不純度指標を以下とする。y_hat はノードにおけるサンプルの平均値。

$\begin{eqnarray*} I ( t ) = \frac {1} {N_{t}} \sum_{i \supseteq D_{t}} ( y_{i} - \hat{y_{t}} )^2 \end{eqnarray*}$

def _mse(self, target):
    y_hat = np.mean(target)
    return np.square(target - y_hat).mean()

二分木では, 親ノードの分散から2つの子ノードの分散の和を引いた値 (目的関数) が最大となる場合を分岐関数とする。

scikit-learn

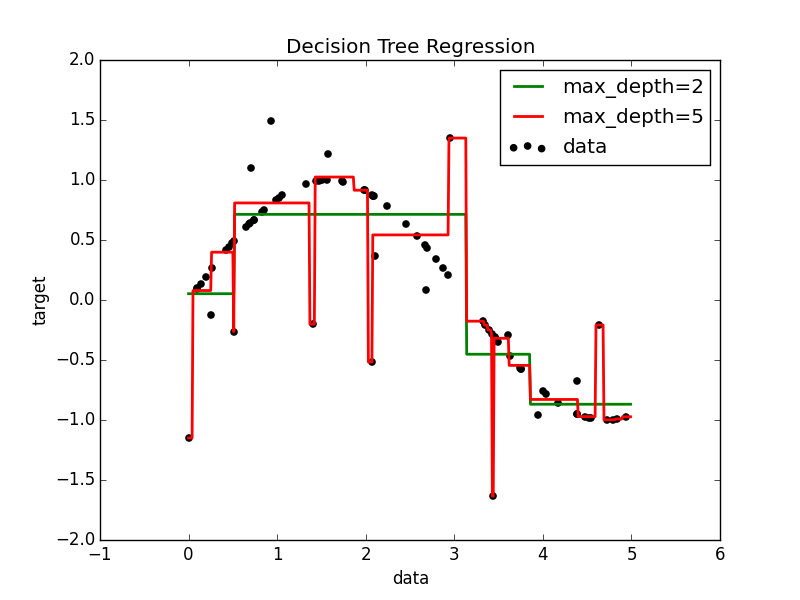
scikit-learn のDecisionTreeRegressorクラスの例 Decision Tree Regression を見てみる。

sin波にノイズを含んだ80点のデータで x の値から高さ y を予測する。例のコードをそのまま動かすと, 以下のような分離超平面がプロットされる。

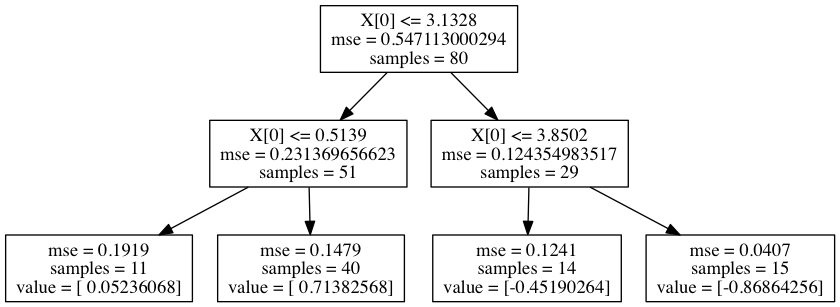
max_depth=5 の場合は過学習していることがわかる。max_depth=2 の決定木を可視化してみる。

前回の分類木と同様に, この得られた決定木 (max_depth=2) と同等の木を得るためのコードを書いてみる。

Python で回帰木を書いてみる

分類木のコードと共通点は多く, ノードの不純度計算を MSE に変更し, 分類木の時は結果をサンプル中に最も多いクラスとしていたのを, 回帰木ではサンプル中の平均値に変更した。早速, 動かしてみる。

# -*- coding: utf-8 -*-

import sys
import os
sys.path.append(os.path.join('./decision-tree/'))

import decision_tree as dt
import numpy as np


def main():
    # Create a random dataset
    rng = np.random.RandomState(1)
    X = np.sort(5 * rng.rand(80, 1), axis=0)
    y = np.sin(X).ravel()
    y[::5] += 3 * (0.5 - rng.rand(16))

    # Fit regression model
    tree = dt.DecisionTreeRegressor(
                criterion='mse',
                pre_pruning=False,
                pruning_method='depth',
                max_depth=2
           )
    tree.fit(X, y)
    tree.show_tree()

    pred = tree.predict(np.sort(5 * rng.rand(1, 1), axis=0))
    print(pred)


if __name__ == '__main__':
    main()

scikit-learn と同じルールの決定木が得られた。

$ python regressor-example.py
 if X[0] <= 3.13275045531
    then if X[0] <= 0.513901088514
        then {value: 0.0523606779563, samples: 11}
        else {value: 0.713825681714, samples: 40}
    else if X[0] <= 3.85022857897
        then {value: -0.451902639773, samples: 14}
        else {value: -0.868642556986, samples: 15}

Code は GitHub に置いた。