【R / lme4】線形混合効果モデル

今回は, 『経時データ解析 (統計解析スタンダード)』に出てくる線形混合効果モデルについての備忘録です。

線形混合効果モデルは複数の被験者で繰り返し測定する経時データや実験計画における空間的相関のある分割区画実験などで用いられる。
分野によっては, 同じモデルをマルチレベルリニアモデル, 階層線形モデル, 潜在変数モデルと呼ぶこともあるようだ。

経時データ

経時データは, 複数の対象者に対しある反応変数を時間の経過とともに繰り返し測定したデータ。同一対象者内の測定値には相関があるため, 分散共分散構造を考慮する必要がある。時系列データの株価も複数時点のデータであるが, 経時データは数時点の測定データである。また, 経済学分野ではパネルデータとも呼ばれる。

線形モデル

線形モデルの内, 一般線形モデル (general linear model)は誤差が正規分布に従うモデルで, 誤差の正規性, データ間の独立性などを仮定している。βをパラメータベクトル, Xはデザイン行列として下記のように表せる。一般的な重回帰モデル。

$\begin{eqnarray*} Y = X^{T}　\beta + \epsilon \end{eqnarray*}$

一般線形モデルに似た言葉として一般化線形モデル (generalized linear model: GLM) がある。一般線形モデルは一般化線形モデルの一部と考えることができる。
GLMは反応変数(または目的変数)が, 正規分布以外にも, 2項分布, ポアソン分布, ガンマ分布などを含む指数型分布族に従う。
ポイントは反応変数の期待値と説明変数の線形成分を, 単調かつ微分可能なリンク関数 g で関連付ける点。これにより, [0,1] や離散値を扱える。μ = E(Y) とした時にリンク関数を用いて下記のように表せる。

$\begin{eqnarray*} g ( \mu ) = X^{T} \beta \end{eqnarray*}$

線形混合効果モデル

線形混合効果モデル (linear mixed-effects model)は, 一般線形モデルを変量効果 (random effects) 及び誤差構造に関して拡張したモデルで, 説明変数に固定効果 (fixed effects) と変量効果を含む。線形混合効果モデルは対象者ごとの反応が独立であると仮定する。

i番目の対象者 (i=1,..,N) の j時点目 (j=1,..,ni) の反応を以下のようなベクトル表記で表す。

$\begin{eqnarray*} Y_{i} = ( Y_{i1}, ... , Y_{in_{1}})^{T} \end{eqnarray*}$

固定効果は反応変数 Yi の平均構造に関係し, 変量効果は Yi の分散共分散構造に関係している。したがって, 固定効果の推定値と変量効果の値では解釈が変わってくる。[1]
固定効果と変量効果はあまりわかりやすいものでなく, データ解析のための統計モデリング入門 [2] でも触れられているように, まずはパラメータには大域的なものと局所的なものがあると考えるのも良さそう。

βは固定効果のパラメータベクトル, b は変量効果のパラメータベクトル, Zはデザイン行列で, b と ε は MVN(0, σΣ) に従うと仮定する。

$\begin{eqnarray*} Y_{i} = X_{i}^{T} \beta + Z_{i} b + \epsilon_{i} \end{eqnarray*}$

より詳しい内容は本書を参考に。

Rで線形混合効果モデル

Rで線形混合効果モデルを作るには {lme4}, {mlmRev} などがある。非線形混合効果モデルは lme4::nlmer(), {nlme} , 一般化線形混合モデルは lme4::glmer() などがあるようだ。いずれもWebに役立つ情報があり, 今回は特に新しい内容を含んではいないが個人的な忘備録ということで…

今回は {lme4} を試してみる。{lme4} パッケージが持つデータセットの一覧を見てみる。

> print(data(package = "lme4"))
Data sets in package ‘lme4’:

Arabidopsis                Arabidopsis clipping/fertilization data
Dyestuff                   Yield of dyestuff by batch
Dyestuff2                  Yield of dyestuff by batch
InstEval                   University Lecture/Instructor Evaluations by Students
                           at ETH
Pastes                     Paste strength by batch and cask
Penicillin                 Variation in penicillin testing
VerbAgg                    Verbal Aggression item responses
cake                       Breakage Angle of Chocolate Cakes
cbpp                       Contagious bovine pleuropneumonia
grouseticks                Data on red grouse ticks from Elston et al. 2001
grouseticks_agg (grouseticks)
                           Data on red grouse ticks from Elston et al. 2001
sleepstudy                 Reaction times in a sleep deprivation study

sleepstudy を使ってみる。下記の変数を持つ。

Reaction: Average reaction time (ms)
Days: Number of days of sleep deprivation
Subject: Subject number on which the observation was made.

ざっくりと Reaction を反応変数, Days を説明変数, Subject を対象者の番号と考える。

lmer() は反応変数 ~ 固定効果 + (変量効果 | 対象者やグループ) のように記述し, 変量効果の項はデザイン行列から (|) により対象者ごとに区別される。

パラメータ推定は, 制限付き最尤法 (REstricted Maximum Likelihood: REML)がデフォルトとなっている。
最尤法 (ML) の分散成分の推定は, 固定効果を推定する際の自由度を考慮しないために偏りがでる場合があるため, 不偏推定値が得られる可能性があるREMLが用いられる事があるらしい。つまり, 線形混合効果モデルのパラメータ推定では REML の方が最尤推定量よりも望ましい推定量になる場合があるため。[3]

data <- data.frame(sleepstudy)

ric.model <- lmer(Reaction ~ Days + (Days | Subject), data = data)
summary(ric.model)
# Linear mixed model fit by REML ['lmerMod']
# Formula: Reaction ~ Days + (Days | Subject)
#    Data: data
#
# REML criterion at convergence: 1743.6
#
# Scaled residuals:
#     Min      1Q  Median      3Q     Max
# -3.9536 -0.4634  0.0231  0.4634  5.1793
#
# Random effects:
#  Groups   Name        Variance Std.Dev. Corr
#  Subject  (Intercept) 612.09   24.740
#           Days         35.07    5.922   0.07
#  Residual             654.94   25.592
# Number of obs: 180, groups:  Subject, 18
#
# Fixed effects:
#             Estimate Std. Error t value
# (Intercept)  251.405      6.825   36.84
# Days          10.467      1.546    6.77
#
# Correlation of Fixed Effects:
#      (Intr)
# Days -0.138

変量効果は lme4::ranef() で得られる。また, 固定効果は summary()で表示されるが lme4::fixef() でも確認できる。

ranef(ric.model)
# $Subject
#     (Intercept)        Days
# 308   2.2585654   9.1989719
# 309 -40.3985770  -8.6197032
# 310 -38.9602459  -5.4488799
# 330  23.6904985  -4.8143313
# 331  22.2602027  -3.0698946
# 332   9.0395259  -0.2721707
# 333  16.8404312  -0.2236244
# 334  -7.2325792   1.0745761
# 335  -0.3336959 -10.7521591
# 337  34.8903509   8.6282839
# 349 -25.2101104   1.1734143
# 350 -13.0699567   6.6142050
# 351   4.5778352  -3.0152572
# 352  20.8635925   3.5360133
# 369   3.2754530   0.8722166
# 370 -25.6128694   4.8224646
# 371   0.8070397  -0.9881551
# 372  12.3145394   1.2840297

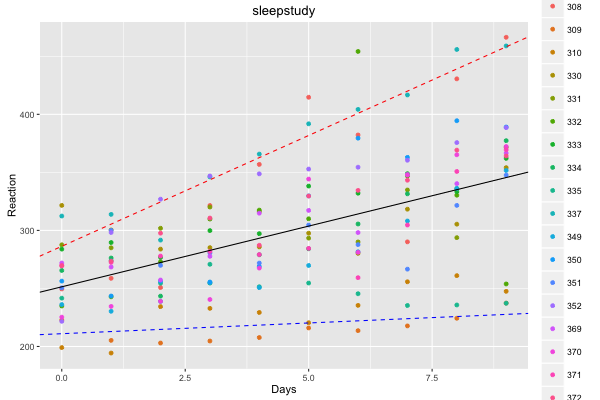
プロットしてみる。黒の実線は固定効果による回帰直線, 破線は固定効果に加えて変量効果(青: 309番, 赤: 337番)が入っている。

AIC, BIC, 尤度比検定 (Likelihood ratio tests) などによるモデル選択。

anova(null.model, ric.model, ri.model)
# refitting model(s) with ML (instead of REML)
# Data: data
# Models:
# null.model: Reaction ~ 1 + (1 | Subject)
# ri.model: Reaction ~ Days + (1 | Subject)
# ric.model: Reaction ~ Days + (Days | Subject)
#            Df    AIC    BIC  logLik deviance   Chisq Chi Df Pr(>Chisq)
# null.model  3 1916.5 1926.1 -955.27   1910.5
# ri.model    4 1802.1 1814.8 -897.04   1794.1 116.462      1  < 2.2e-16 ***
# ric.model   6 1763.9 1783.1 -875.97   1751.9  42.139      2  7.072e-10 ***
# ---
# Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

最尤推定で Re-fitting したい場合は, update() で PEML = FALSE を指定する。

ric.model.ML <- update(ric.model, REML = FALSE)

Code は GitHub に置いた。

[1] 生態学のデータ解析 – ランダム効果とは?
[2] データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)
[3] 制限付き最尤法 (REML)
[4] Fitting Mixed-Effects Models Using the lme4 Package in R
[5] 生態学のデータ解析 – GLM 参照
[6] 経時測定データの解析
[7] 混合効果モデル（変量効果モデル、mixed effect model）について
[8] Linear Mixed Model （以下、混合モデル）の短い解説
[9] 線形混合効果モデルメモ