今回は離散選択モデルのひとつ, 多項ロジットモデルについて書きます。
離散選択モデル
複数の選択肢の集合から, 1つを選択する場合の数理モデルを離散選択モデル (discrete choice model) という。
【R】順序ロジットモデルと順序プロビットモデル【比例オッズ】でも触れた, 目的変数が順序尺度でなく選択肢が3つ以上の場合の代表的なモデルとして, ロジスティック分布を使う多項ロジットモデル (multinomial logit model, MNL)と, 正規分布を使う多項プロビットモデル (multinomial probit model, MNP)がある。
多項ロジットモデルは IIA特性 (Independence from Irrelevant Alternatives, 無関係の選択肢からの独立性) を仮定する。これは, “ある2つの選択肢のオッズ比が, 他の選択肢が選択可能かに左右されない”という中々強い仮定である。一方, 多項プロビットモデルは誤差項の相関構造を仮定することで IIA を回避できるが, 多項ロジットモデルと比べて計算量は多くなる。
応用例としては, 社会学や心理学, 計量経済学, 交通工学[1], マーケティング分野などがあり, 例えば複雑な要因から消費者がある商品を選択した根拠を読み解く際に使われている。
Rで多項ロジットモデル
{mlogit} を使って, 多項ロジットモデルを試してみる。
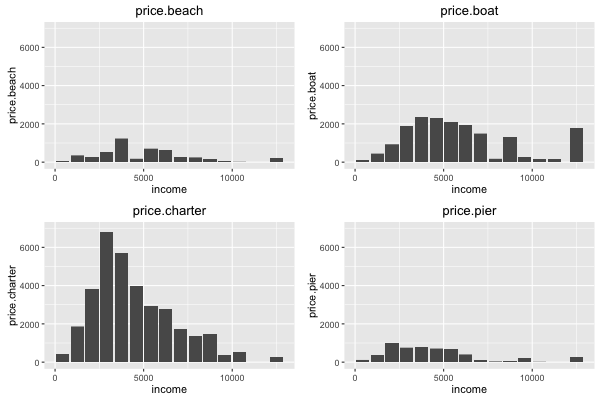
今回使う Fishing データセットはクロスセクションデータで下記から成る。
- mode: 意思決定者は {beach, pier(桟橋), boat, charter} の集合から1つだけ選択
- price: mode に対する価格
- catch: mode における漁獲率
- income: 意思決定者の月収
- chid: 意思決定者のID
元のdata.frameを確認する。1人につき1行となっている。
> head(Fishing)
mode price.beach price.pier price.boat price.charter catch.beach catch.pier catch.boat catch.charter income
1 charter 157.930 157.930 157.930 182.930 0.0678 0.0503 0.2601 0.5391 7083.332
2 charter 15.114 15.114 10.534 34.534 0.1049 0.0451 0.1574 0.4671 1250.000
3 boat 161.874 161.874 24.334 59.334 0.5333 0.4522 0.2413 1.0266 3750.000
4 pier 15.134 15.134 55.930 84.930 0.0678 0.0789 0.1643 0.5391 2083.333
5 boat 106.930 106.930 41.514 71.014 0.0678 0.0503 0.1082 0.3240 4583.332
6 charter 192.474 192.474 28.934 63.934 0.5333 0.4522 0.1665 0.3975 4583.332
incomeによって各modeのpriceは異なっている。
この data.frame を, mlogit()のために適した形に変形する。
# shape a data.frame in a suitable form for the use of the mlogit function.
Fish <- mlogit.data(Fishing, varying = c(2:9), shape = "wide", choice ="mode")
変形後は mlogit.data クラスの属性が追加された。
# class() でも同様
> attributes(Fishing)$class
[1] "data.frame"
> attributes(Fish)$class
[1] "mlogit.data" "data.frame"
各行は4つの mode についてそれぞれ 選択した/しない で複数行に分割されて, 1人で4行となった。その分, 列名がすっきりしている。
> head(Fish)
mode income alt price catch chid
1.beach FALSE 7083.332 beach 157.930 0.0678 1
1.boat FALSE 7083.332 boat 157.930 0.2601 1
1.charter TRUE 7083.332 charter 182.930 0.5391 1
1.pier FALSE 7083.332 pier 157.930 0.0503 1
2.beach FALSE 1250.000 beach 15.114 0.1049 2
2.boat FALSE 1250.000 boat 10.534 0.1574 2
mlogit()でモデリング。結果には対数尤度, McFadden's R-squared, 尤度比検定 が含まれる。
model <- mlogit(mode ~ price | income | catch, Fish)
summary(model)
# Coefficients :
# Estimate Std. Error t-value Pr(>|t|)
# boat:(intercept) 8.4184e-01 2.9996e-01 2.8065 0.0050080 **
# charter:(intercept) 2.1549e+00 2.9746e-01 7.2443 4.348e-13 ***
# pier:(intercept) 1.0430e+00 2.9535e-01 3.5315 0.0004132 ***
# price -2.5281e-02 1.7551e-03 -14.4046 < 2.2e-16 ***
# boat:income 5.5428e-05 5.2130e-05 1.0633 0.2876612
# charter:income -7.2337e-05 5.2557e-05 -1.3764 0.1687088
# pier:income -1.3550e-04 5.1172e-05 -2.6480 0.0080977 **
# beach:catch 3.1177e+00 7.1305e-01 4.3724 1.229e-05 ***
# boat:catch 2.5425e+00 5.2274e-01 4.8638 1.152e-06 ***
# charter:catch 7.5949e-01 1.5420e-01 4.9254 8.417e-07 ***
# pier:catch 2.8512e+00 7.7464e-01 3.6807 0.0002326 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Log-Likelihood: -1199.1
# McFadden R^2: 0.19936
# Likelihood ratio test : chisq = 597.16 (p.value = < 2.22e-16)
Fishに対するフィットの確認。
head(model$fitted.values)
# 1.beach 2.beach 3.beach 4.beach 5.beach 6.beach
# 0.3114002 0.4537956 0.4567631 0.3701758 0.4763721 0.4216448
head(model$probabilities)
# beach boat charter pier
# [1,] 0.09299769 0.5011740 0.3114002 0.09442817
# [2,] 0.09151070 0.2749292 0.4537956 0.17976449
# [3,] 0.01410358 0.4567631 0.5125571 0.01657625
# [4,] 0.17065868 0.1947959 0.2643696 0.37017585
# [5,] 0.02858215 0.4763721 0.4543225 0.04072324
# [6,] 0.01029791 0.5572463 0.4216448 0.01081103
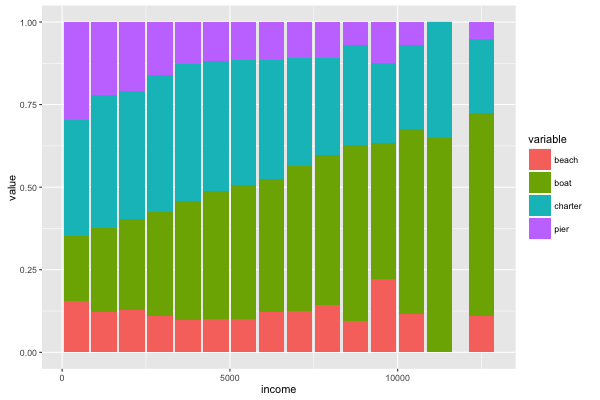
incomeに対する各modeの予測選択確率をまとめると, 下記のようになった。
未知のデータを予測する場合。
unknown <- Fish[1:4,]
unknown[1:4,]$income <- 2000
predict(model, newdata = unknown)
# beach boat charter pier
# 0.08386158 0.34096752 0.40560746 0.16956344
Code は GitHub に置いた。
多項プロビットモデルの他に IIA特性 を回避するモデルとして, ネステッド・ロジットモデルなどがある。
[1] 基礎オペレーションズリサーチ (別冊)
[2] ネスティッドロジットモデルとIIA特性 singular point
[3] 多項ロジット(Multinomial Logit), R - mlogit 使用メモ - 東京に棲む日々
[4] Comparing mnlogit and mlogit for discrete choice models R-bloggers
[5] Rで学ぶ離散選択モデル
[6] マーケティングサイエンスにおける離散選択モデルの展望