【forecast】Rでファイナンスデータの時系列分析

計量時系列分析について調べたこと, 主に AR, ARMA, ARIMA モデルについてメモを残します。

ファイナンスデータの準備

今回は Yahoo!ファイナンス から日産自動車 [7201] のデータを取得しました。

分析の前に csv の文字コードを Shift_JIS から utf-8 に変更しておきます。OS X の場合 nkf コマンドを使います。

$ brew install nkf
$ nkf -w --overwrite ./data/7201.T.csv

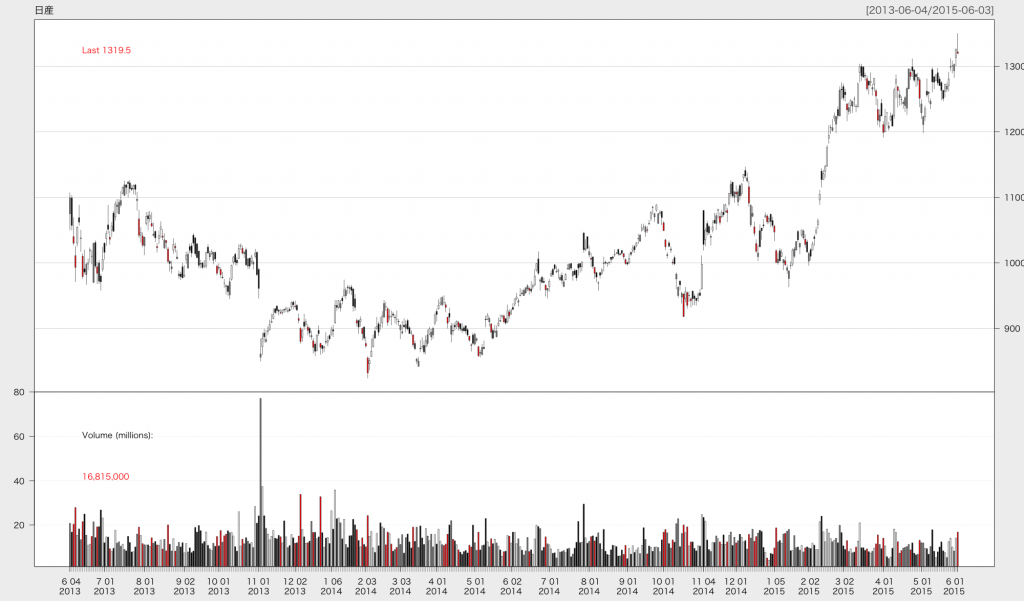
まずは, {quantmod} でロウソク足を図示してみます。

library(quantmod)

# convert char-code "nkf -w --overwrite filename"
df <- read.csv("data/7201.T.csv", header = T)
names(df) <- c("Date", "Open", "High", "Low", "Close", "Volume", "Adjusted")

head(df)
#       Date   Open   High    Low  Close   Volume  Adjusted
# 1  2015/6/3 1322.0 1350.0 1319.5 1319.5 16815000   1319.5
# 2  2015/6/2 1313.0 1326.5 1300.5 1326.0 14139600   1326.0
# 3  2015/6/1 1293.0 1304.0 1282.5 1302.5  8270000   1302.5
# 4 2015/5/29 1300.0 1308.5 1289.5 1300.5 10061300   1300.5
# 5 2015/5/28 1298.5 1312.0 1293.0 1299.0 14069200   1299.0
# 6 2015/5/27 1270.0 1291.0 1262.0 1280.5 12494400   1280.5

candle_stick <- read.zoo(df, header = T)

par(family = "HiraKakuProN-W3")
candleChart(candle_stick, name = "日産自動車", multi.col = TRUE, theme = "white")

7201.T

data.frame の日付と終値から time-series object を作ります。

df.zoo <- zoo::zoo(df$Close, order.by = as.Date(df$Date, format = '%Y/%m/%d'))
# to create time-series object
df.ts <- ts(df.zoo)

時系列解析

時系列解析 (Time Series Analysis) はある現象の変動を過去の動きとの関連で捉えようとするものです。時系列解析を行う上で, 時系列データが定常過程か非定常過程かが最初のポイントとなります。

  • 定常 (Stationarity): 一見したところ不規則な現象でも時間的に変化しない一定の確率モデルの実現値とみなせるような平均や分散が時間変化しない時系列。 (e.g., 白色雑音)
  • 非定常 (Non-Stationarity): 平均の周りの変動の仕方が時間的に変化している時系列。平均や分散の時間変化がある場合。

定常は平均と分散が時間変化せずに自己相関が時間差のみに依存する性質を指します。また, 定常性は長期的には平均への回帰を期待しているとも言えます。

tseries::adf.test() で単位根検定のひとつである拡張ディッキー–フラー検定 (Augmented Dickey–Fuller test; ADF test) を行います。

tseries::adf.test(df.ts)
# Augmented Dickey-Fuller Test
#
# data:  df.ts
# Dickey-Fuller = -2.6838, Lag order = 10, p-value = 0.2889
# alternative hypothesis: stationary

原系列は非定常過程のようです。原系列が非定常の場合でも, その d 階差は定常となる場合があります。

df.diff <- diff(log(df.ts))

tseries::adf.test(df.diff)
# Augmented Dickey-Fuller Test
#
# data:  df.diff
# Dickey-Fuller = -11.138, Lag order = 10, p-value = 0.01
# alternative hypothesis: stationary

p値が 0.01 であることから差分系列は定常過程と考えて良さそうです。

時系列モデル

今回のような株価や為替のデータの場合, あまりに古いデータから使ってしまうと経済・金融政策などの前提が大きく変化していることがあり返って予測精度を落とす場合があります。今回はリーマンショック以降の 2010 年以降のデータでモデリングしてみます。

今回扱うモデルは以下です。

  • AR: 自己回帰モデル
  • ARMA: 自己回帰移動平均モデル
  • ARIMA: 自己回帰和分移動平均モデル

ARモデル

AR (Autoregressive) モデルは過去の観測値から定まるモデルで, 自己回帰の次数 p と自己回帰係数 a として以下で表されます。

    \begin{eqnarray*} y_n = \sum_{i=1}^p a_i y_{n-1} + v_n \end{eqnarray*}

AR モデルは自身の時系列の過去の値を用いた重回帰モデルとも解釈できます。stats::ar() は特に指定しない限り AIC が最小となるようにラグ次数を求めます。

ARMAモデル

ARモデルに移動平均 MA の項を追加したのが ARMA (Autoregressive and Moving Average) モデルで, 移動平均の次数 q, 移動平均係数 b として以下となります。

    \begin{eqnarray*} y_n = \sum_{i=1}^p a_i y_{n-1} + v_n - \sum_{i=1}^q b_i v_{n-1} \end{eqnarray*}

ARMA モデルの動機のひとつは大きくなりやすい AR の次数 p を減らすためで移動平均 (Moving Average; MA) により平滑化します。AR と MA は異なる自己相関のパターンを表現できます。stats::arima() で ARMA モデルを構築できます。

ARIMAモデル

ARIMA (Autoregressive, Integrated and Moving Average) は AR, Integrated (和分), MA で構成されます。ARMA に和分が追加されています。和分とは定常な時系列を得るために時系列の観測値の階差を取るプロセスを指します。原系列 d-1 が非定常過程であっても, d 階差分をとった過程が定常過程となる場合を d 次和分過程と言います。

ARIMA は近似的に定常な時系列が得られるまで d 階差分をとり, その時系列に ARMA を適用します。 ARIMA(p, d, q) のように表し ARIMA(p, 0, q) の場合に ARMA(p, q) と一致します。

library(forecast)
# Plots a time series along with its acf (AutoCorrelation Function) and either its pacf (Partial ACF),
# lagged scatterplot or spectrum.
par(family="HiraKakuProN-W3")
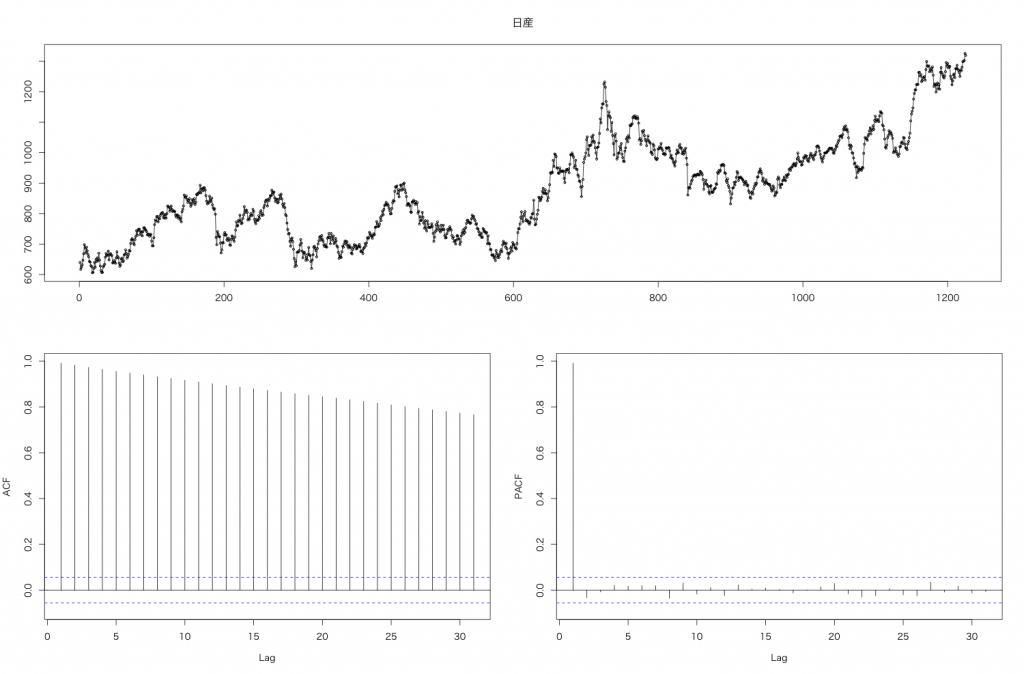
tsdisplay(df.ts, main = "日産")

model <- auto.arima(
    df.ts,
    max.p = 2, # AR degree
    max.q = 2, # MA degree
    ic = "aic",# model selection.
    trace = T, # reported option
    stepwise = T
)

summary(model)

forecast::tsdisplay() でACF, PACFをプロットします。

ACF (自己相関関数) は自身のラグの時系列との相関, PACF (偏自己相関係数) は時系列とそれ以前のラグでは説明できない相関相関量です。

ACF

forecast::auto.arima() で ARIMA のモデル選択を自動で行います。ic にはモデル選択に用いる情報量基準を指定します。AICの場合は以下です。

model <- auto.arima(
    df.ts,
    max.p = 2, # AR degree
    max.q = 2, # MA degree
    ic = "aic",# model selection.
    trace = T, # reported option
    stepwise = T
)

summary(model)
# ARIMA(2,1,2) with drift         : 11139.28
# ARIMA(0,1,0) with drift         : 11134.47
# ARIMA(1,1,0) with drift         : 11136.04
# ARIMA(0,1,1) with drift         : 11135.78
# ARIMA(0,1,0)                    : 11133.21
# ARIMA(1,1,1) with drift         : 11137.57
#
# Best model: ARIMA(0,1,0) with drift

ARIMA(0, 1, 0) が選択されました。これは1階差分の AR(0), MA(0) です。

sigma^2 estimated as 260.4:  log likelihood=-5136.17
AIC=10276.34   AICc=10276.35   BIC=10286.56

Training set error measures:
                       ME     RMSE      MAE         MPE     MAPE     MASE
Training set 0.0005219955 16.12392 12.06049 -0.02388146 1.412625 1.000159
                   ACF1
Training set 0.02431441
Training set 0.09790725

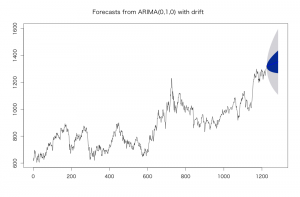
forecast() で予測を行います。level で信頼区間の幅を指定, h で予測する期間を指定できます。

f <- forecast(
    model,
    level = c(50, 95), # confidence interval
    h = 20 * 3 # after 3 months
)
plot(f)

ARIMA

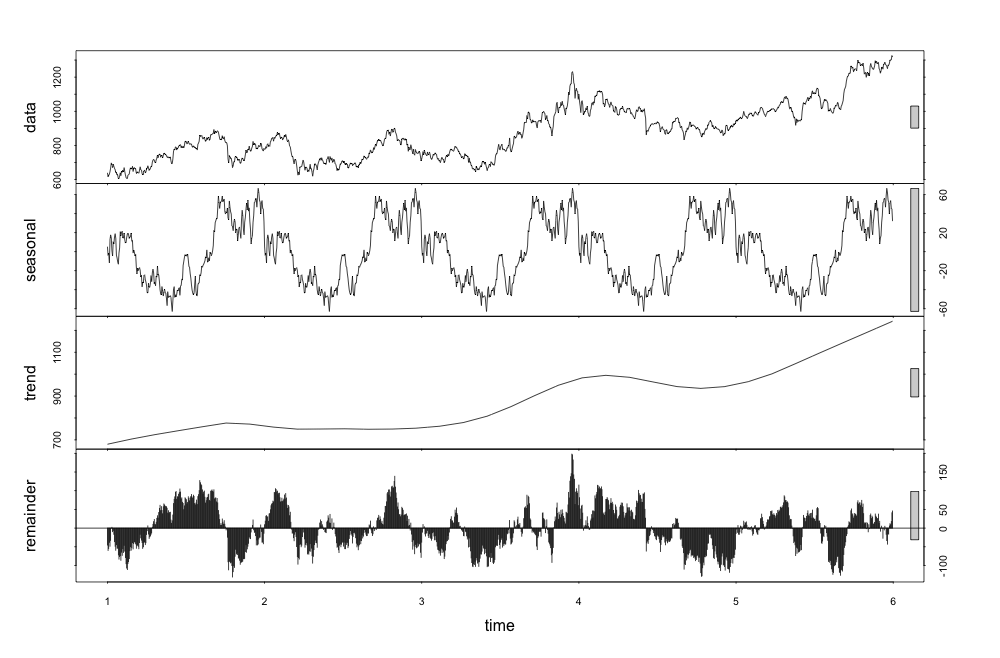
stl() で原系列を 季節変動 + トレンド + 残差 に分解して図示してみます。

df.ts <- ts(df.zoo, frequency = 245)
# data = seasonal + trend + residualError
stl <- stl(df.ts, "periodic")
plot(stl)

trend

Code は GitHub にあります。

おわりに

AR, ARMA, ARIMA は単変量を扱う時系列モデルで, この他に単変量を扱うモデルには GARCH があります。 また, 多変量を扱う時系列に VAR (Vector Autoregressive) モデルなどがあります。
一方, ARIMA は時系列の挙動あるいは変動要因に対して解釈を与えるのに難があるという見方もあり, モデリングの柔軟性と増減要因の説明力という点において状態空間モデルに利点があります。状態空間モデルは観測方程式と状態方程式を組み合わせたモデルで, 状態空間モデルは AR, ARMA, ARIMA を内包します。

参考書籍は『時系列解析入門』, 『経済・ファイナンスデータの計量時系列分析』, 『ファイナンスのためのRプログラミング』の3冊です。


[1] Rで計量時系列分析：AR, MA, ARMA, ARIMAモデル, 予測
[2] Rで計量時系列分析：単位根過程、見せかけの回帰、共和分、ベクトル誤差修正モデル